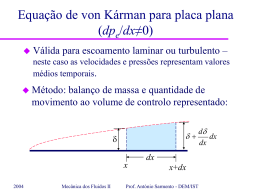
Equação de von Kárman para placa plana
(dpe/dx≠0)
 Válida
para escoamento laminar ou turbulento –
neste caso as velocidades e pressões representam valores
médios temporais.

Método: balanço de massa e quantidade de
movimento ao volume de controlo representado:
d

dx
dx

dx
x
2004
Mecânica dos Fluidos II
x+dx
Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
d
M VC   m x  m   m x  dx
 Balanço de massa:
dt
m 
Esc. estacionário
m x
m x  dx
dx
o Caudal
o Caudal
2004
m x :



m x    udy
0
x
m x  dx : m x  dx


d 
  udydx

dx  0





d 
   udy    udydx
0
 x dx  0

Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
 Balanço
de massa:


d 
m     udydx
dx  0

m 
m x
m x  dx
dx
o Caudal de quantidade de movimento segundo x através y=δ:
qqm x
2004



d
 Um   U   udydx
dx  0

Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
 Balanço
de q. movimento segundo x:
dKxVC
dt


 qqmx x  qqmx  qqmx x  dx  FxVC
qqmx 
esc. estacionário
qqmx x qqmx xdx
o Diferença qqmx xdx  qqmx x :
2004
Mecânica dos Fluidos II


d 
2

   u dy dx
dx  0

Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
 Balanço
de q. movimento segundo x:


FxVC  qqmx x dx  qqmx x  qqmx


d 
2
  u dy dx

dx  0



d 
  udydx
U

dx  0

qqmx 
qqmx x qqmx xdx
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
 Forças
FxVC
segundo x:
1 

 p   p  dp  d    p  dpd   0 dx
2 

FxVC
dp 

  0  
dx
dx 

dp e
dU
  U
dx
dx
p+1/2dp
p
p+dp
τ0
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
 Resultado:



dU
 0    U  u udy 
 U  u dy

x 0
dx 0
 Introduzindo d e δm:


d
dU
2
0 
U  m  U d
dx
dx
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx=0)
 Caso
em que dpe/dx=0 (dU/dx=0):
d m
 0  U
dx
2
0
d m
cf 
2
1
dx
U 2
2
dpe/dx=0 (dU/dx=0) vem m=a
(a diferente em CL laminar e turbulenta):
 Quando
d
c f  2a
dx
2004
Mecânica dos Fluidos II
A CL cresce mais rapidamente
quando Cf é maior
Prof. António Sarmento - DEM/IST
Soluções aproximadas da CL laminar para
dpe/dx=0
 A solução
de Blasius mostrou que
y
com  
Re x
x

e que   5
x
Re x
u

 m    1 
U
0
1
 u  y
 d 
U  
u
 f  
U
y 5x y
5
x

u
 y
 f 
U
 
a – constante em toda a CL
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Soluções aproximadas da CL laminar para
dpe/dx=0
 Equação
de von Kárman:  0  U 2
mas
 u 
U
 0      

 y  y 0
d m
2 d
 U a
dx
dx
 d u U  
U


 

 d  y    y  0
β - constante

x

2004
2
a
1
Re x
Integrando
 0  0
Mecânica dos Fluidos II
d
   U a

dx
U
2
Prof. António Sarmento - DEM/IST
Soluções aproximadas da CL laminar para
dpe/dx=0
 Vimos
que  0  
e

x

2004

U

0
2
cf 

2
U 2 U

2
a
1
Re x
2 a
cf 
Re x
2 a
CD  2
Re L
Nota: a e β dependem da forma do perfil, contudo δ/x,
cf e CD variam pouco com a forma do perfil.
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Soluções aproximadas da CL laminar
para dpe/dx=0
Perfis aproximados para CL laminar com
a  m 
  d u U  d  y  y  0
Linear
a
u
y

U 
Parabólico
u
y  y
 2  
U
  
Sinusoidal
u
 y 
 sin 

U
2
0,167
β
1
2
Blasius
2004
dp e dx  0
Mecânica dos Fluidos II
0,133
2
0,137

2
 x
cf
3,461
0,578
Re x
Re x
5,484
0,729
Re x
Re x
4,789
0,656
Re x
Re x
5
0,664
Re x
Re x
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Matéria:
– Equação de von Kármàn;
dpe
– Simplificação para o caso
0 ;
dx
dpe
 0.
– Solução aproximada passa C.L. Laminar com
dx
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Bibliografia:
– Sabersky – Fluid Flow: 8.6, 8.7
– White – Fluid Mechanics: 7.3, 7.4
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Problema sobre a Eq. Von Kármàn
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST