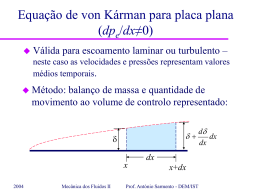
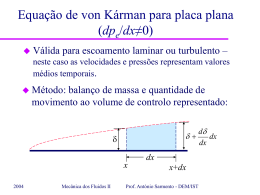
Introdução ao escoamento não-estacionário
em condutas

Matéria:
– Escoamentos não-estacionários: exemplo
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Escoamentos não-estacionários: Exemplo

Tanque com superfície livre de altura h (constante) esvazia através de
tubagem de diâmetro d, comprimento l e comprimento equivalente (l/d)eq .
Qual o caudal em regime permanente? Quanto tempo demora a tingir 99%
desse caudal desde abertura da válvula (t=0)?
z
A
1
h
2
válvula
q
3
R: a) Equação da continuidade:
dM tubo
 m 2  m 3
dt
V  V t  constanteao longodo tubo
  cte. e tubo indeformável
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Escoamentos não-estacionários: Exemplo

Tanque com superfície livre de altura h (constante) esvazia através de
tubagem de diâmetro d, comprimento l e comprimento equivalente (l/d)eq .
Qual o caudal em regime permanente?
z
A
1
h
2
válvula
Qs
3
Eq. Bernoulli generalizada
(regime permanente)
3
 p V2
  p V2

1 V



  H  h
dl



z



z




g 1 t
 g 2 g
3  g 2 g
1
Vest 
l V
f 
 d eq 2 g
2004
Mecânica dos Fluidos II
2
Prof. António Sarmento - DEM/IST
2 g z1  z3 
l
1 f  
 d  eq
Escoamentos não-estacionários: Exemplo

z
A
1
h
válvula
2
Quanto tempo demora a tingir
99% desse caudal desde abertura
da válvula (t=0)?
Qs
3
R: b) Eq. Bernoulli generalizada
3
 p V2
  p V2

1 V
dl  

 z   

 z   H  h

g 1 t
 g 2 g
3  g 2 g
1
V
V
  dl   dl
t
t
1
2
2
2004
l V
f 
 d eq 2 g
3
Mecânica dos Fluidos II
2
V  V t 
Prof. António Sarmento - DEM/IST
dV
l
dt
Escoamentos não-estacionários: Exemplo
z

A
1
h
válvula
2
Quanto tempo demora a tingir
99% desse caudal desde abertura
da válvula (t=0)?
Qs
3
Eq. Bernoulli generalizada
l dV V 2 

1 
g dt 2 g 
2l
dV
 Vest2  V 2
 l  dt
1 f  
 d  eq
Vest 
l
1 f  
dV
 d eq

dt
2
2
Vest  V
2l
2004
Mecânica dos Fluidos II
l 
f     z1  z3
 d  eq 
2 g z1  z3 
l
1 f  
 d  eq
l
1

f
  t
V
dV
 d eq
0 Vest2  V 2  2l 0 dt
Prof. António Sarmento - DEM/IST
Escoamentos não-estacionários: Exemplo
z

A
1
h
válvula
2
t
Qs
3
Continuação:
l
1

f
  t
V
dV
 d eq
0 Vest2  V 2  2l 0 dt
V V
2l
1
ln est
1  f l d eq 2Vest Vest  V
Para V=0,99Vest: t 
Quanto tempo demora a tingir
99% desse caudal desde abertura
da válvula (t=0)?
dx
1
ax
 a 2  x 2  2a ln a  x
2l
1
1,99
ln
1  f l d eq 2Vest 0,01
5,2933
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Escoamentos não-estacionários: Exemplo
z

A
1
h
válvula
2
Caso concreto: l=100m; d=10cm;
=1mm; z1-z3=20m; (l/d)eq=1200
Qs
3
1ªaproximação: escoamento completamente turbulento: f=0,038
Vest 
2 g z1  z3 
 2,9m / s
l
 
1 f  
 d eq
t
2l
1
1,99
ln
 3,92s
1  f l d eq 2Vest 0,01
Re=2,9 x 105 confirma escoamento completamente turbulento
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introdução ao escoamento não-estacionário
em condutas

Matéria:
– Escoamentos não-estacionários: exemplo
 Bibliografia:
– Secção 13.4, Cap. 13, Fluid Mechanics with Engineering
Applications, Robert L. Daugherty, Joseph B. Franzini, E.
John Finnemore, 8ª Edição, Int. Student Ed., ISBN 0.07015441-4, 1985.
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST