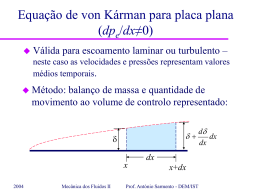
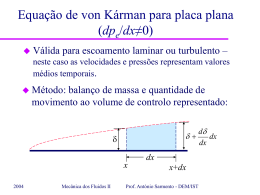
Introdução ao escoamento não-estacionário
em condutas

Matéria:
–
–
–
–
2004
Tipos de escoamentos não-estacionários:
Equações da continuidade e de Bernoulli generalizada
Escoamentos quasi-estacionários: exemplo
Escoamentos não-estacionários: exemplo
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introdução ao escoamento não-estacionário
em condutas

Tipos de escoamentos não-estacionários:
– Escoamentos quasi-estacionários: acelerações locais desprezáveis.
– Escoamentos não-estacionários:
– Golpe de Aríete: forças elásticas do fluido ou da parede da conduta
relevantes.
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equações para escoamentos não-estacionários
em condutas

Equação da continuidade para um VC:
dM VC
 m e  m s
dt
Caudal mássico de saída
Caudal mássico de entrada

Equação de Bernoulli Generalizada:
Energia dissipada por
unidade de peso
s
 p V2
  p V2

1 V



  H  h
dl



z



z




g e t
 g 2 g
 s  g 2 g
e
Energia recebida por
unidade de peso
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Escoamentos quasi-estacionários: Exemplo

Tanque com superfície livre de área A e altura h esvazia através
de orifício de área As na base. Como varia h com o tempo?
z
R: Equação da continuidade:
dM VC
 m e  m s
dt
A
h
Qs
 s  AsVs
m
h
M VC    Az dz
o
dMVC
dh
A
 Ah    dz
dt
dt o t
h
2004
Mecânica dos Fluidos II
dh
Ah    AsVs
dt
Prof. António Sarmento - DEM/IST
Escoamentos quasi-estacionários: Exemplo

Tanque com superfície livre de área A e altura h esvazia através
de orifício de área As na base. Como varia h com o tempo?
z
A
R: Equação Bernoulli generalizada:
h
s
 p V2
  p V2

1 V
dl  

 z   

 z   H  h

g e t
 g 2 g
 s  g 2 g
 sl
Acelerações locais
desprezáveis
Vsl baixa quando
comparada com Vs
Qs
Vs  2 g zsl  zs 
h
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Escoamentos quasi-estacionários: Exemplo
Tanque com superfície livre de área A e altura h esvazia através
de orifício de área As na base. Como varia h com o tempo?

z
R: Equação continuidade: Ah 
dh
  AsVs
dt
Equação Bernoulli generalizada: Vs  2 gh
Ah 
dh   2 g As dt
h
2004
A
Mecânica dos Fluidos II
h t 

h0
Ah 
dh   2 g As t
h
Prof. António Sarmento - DEM/IST
h
Qs
Escoamentos quasi-estacionários: Exemplo

Tanque com superfície livre de área A e altura h esvazia através
de orifício de área As na base. Como varia h com o tempo?
h t 
Se A for constante:
A
ho
2 h
ht   h0  2 g
z
dh
  2 g As t
h
A
h
h t 
h0
As
t
2A
2
h  h0  2 gh0
As
gA 
t   s  t2
A
2 A
V0
Tempo de esvaziamento (h=0): t f 
2004
Mecânica dos Fluidos II
A
As
2 gh0
g
Prof. António Sarmento - DEM/IST
Qs
Escoamentos não-estacionários: Exemplo

Tanque com superfície livre de altura h (constante) esvazia através de
tubagem de diâmetro d, comprimento l e comprimento equivalente (l/d)eq .
Qual o caudal em regime permanente? Quanto tempo demora a tingir 99%
desse caudal desde abertura da válvula (t=0)?
z
A
1
h
2
válvula
Qs
3
R: Equação da continuidade:
dM tubo
 m 2  m 3
dt
 2
  cte. e M tubo   d l
4
2004
Mecânica dos Fluidos II
V  V t  constanteao longodo tubo
Prof. António Sarmento - DEM/IST
Introdução ao escoamento não-estacionário
em condutas

Matéria:
– Escoamentos qausi-estacionários: exemplo
 Bibliografia:
– Secções 13.1 e 13.2, Cap. 13, Fluid Mechanics with
Engineering Applications, Robert L. Daugherty, Joseph B.
Franzini, E. John Finnemore, 8ª Edição, Int. Student Ed.,
ISBN 0.07-015441-4, 1985.
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST