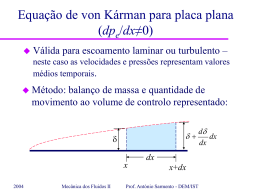
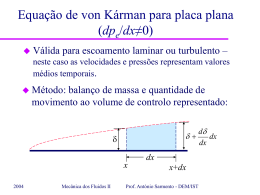
Revisões de Camada Limite Laminar

Matéria:
–
–
–
–
–
–
–
2004
Introdução à Camada limite;
Camada limite confinada e não-confinada;
Escoamentos de corte livre e Esteira;
Camadas limites laminares e turbulentas;
Separação da camada limite;
Equações para CL delgada;
Efeito do gradiente longitudinal sobre a evolução da camada
limite.
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introdução à camada limite
Filmes (6), 88, 89
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introdução à camada limite
 Camada
limite: região na vizinhança de uma parede
onde se fazem sentir os efeitos difusivos e dissipação de
energia mecânica
Escoamento exterior
y
U
U
x
d(x)
Espessura da camada
limite: u(d)=0,99 U
2004
Mecânica dos Fluidos II
Camada limite: u y significativo
Prof. António Sarmento - DEM/IST
Introdução à camada limite
 Linhas
y
U
de corrente sobre uma placa plana:
Linha limite da CL
U
Linha de
corrente
x
1. As linhas de corrente afastam-se lentamente da parede. Porquê?
2. Esse afastamento é mais intenso nas linhas de corrente exteriores
à CL. Porquê?
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introdução à camada limite
 Notas
sobre a camada limite:
1. A camada limite pode ser laminar ou turbulenta.
2. A camada limite diz-se delgada se d(x)<<x
3. A camada limite diz-se confinada se não puder crescer
livremente (ex: num tubo ou entre placas).
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introdução à camada limite
 Camada
Escoamento
exterior
d(x)
limite confinada:
zona de perfil
camada limite
região de entrada desenvolvido
1. Na região de entrada: a velocidade aumenta na zona central (para
manter o caudal) e a pressão baixa (eq. Bernoulli) –> dp/dx<0.
2. Após a união das CL todo o escoamento é de camada limite,
d (x )  R e a dimensão dos vórtices é limitada a d.
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introdução à camada limite
 Camada
limite não-confinada (escoamentos exteriores):
1. d não é limitado, vai crescendo com a distância x (distância ao
início da CL).
2. Perfil de velocidades adimensional pode estabilizar.
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introdução à camada limite
 Outros
escoamentos de corte (transporte convectivo
longitudinal de quantidade de movimento afectado por difusão
transversal):
2004
o
Escoamentos de corte livre: ex: jacto livre
o
Esteira: zona do escoamento resultante da
junção das CL sobre as duas faces da placa
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Introdução à camada limite
 Passagem
de regime laminar a turbulento:
forças inércia Ux
Re =
=
forças viscosas 
• Início da CL:
x – distância ao início da CL
x=0
Re = 0
Escoamento
laminar
 0 =  (u y)y=0 muito elevado
• Placa suficientemente longa:
Passagem a
turbulento
2004
Re crítico
(5105)
Mecânica dos Fluidos II
Re aumenta
 0 =  (u y)y=0 reduz-se
Prof. António Sarmento - DEM/IST
Introdução à camada limite
 Regiões
–
–
–
–
da camada limite turbulenta:
Sub-camada laminar;
Camada de transição;
Zona de perfil logarítmico;
Zona exterior (vórtices turbulentos misturados com
escoamento exterior não-turbulento).
Filmes 2
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equações da camada limite laminar
delgada (d<<x) sobre placa plana
estacionário, r e  constantes.
 p y  0 pois as linhas de corrente são
ligeiramente divergentes
p x  dpe dx
 Escoamento
 Equação
de Navier-Stokes 2D na direcção x:
u
u
1 p   2u  2u 
u v
=
   2  2 
x
y
r x  x y 
dpe dx
2004
Mecânica dos Fluidos II
 2u
quando comparado com 2
y
Prof. António Sarmento - DEM/IST
Equações da camada limite laminar
delgada (d<<x) sobre placa plana
 Equação
de camada limite laminar 2D delgada
(d<<x) para placa plana:
u
u
1 dpe
 2u
u v
=
 2
x
y
r dx
y
pe – pressão exterior, pode ser calculada pela equação de
Bernoulli, visto não haver efeitos viscosos no exterior da CL
Nota 1. A placa pode ser considerada plana de d for muito menor
que o raio de curvatura local
Nota 2. No ponto de separação a CL cresce muito e deixa de ser
delgada.
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equações da camada limite turbulenta
delgada (d<<x) sobre placa plana
 Equação
de camada limite turbulenta 2D delgada
(d<<x) para placa plana:
u
u
1 dpe
 2u  uu uv uw 

u
v
=
 2  


x
y
r dx
y  x
y
z 
0
0
Resultante das
Tensões de Reynolds
(notar o termo em w’)
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da camada limite
 Separação
da camada limite: inversão do escoamento
por acção de um gradiente de pressão adverso (pressão
cresce no sentido do escoamento) + acção viscosa
Filme 41
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da Camada Limite
 Equação
de camada limite laminar 2D delgada
(d<<x) para placa plana:
u
u
1 dpe
 2u
u v
=
 2
x
y
r dx
y

Junto à placa (y=0)
u=v=0 :
  2u 
1 dpe
 2  =
 y  y =0  dx

2004
Mesmo resultado para camada limite turbulenta,
pois junto à placa há a sub-camada laminar.
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da Camada limite
 Exterior
 Junto
da camada limite:
à placa (y=0)
u=v=0 :
  2u 
1 dpe
 2  =
 y  y =0  dx
O
mesmo sinal
gradiente de pressão exterior pode ser:
o
dpe/dx=0 <–> U0 constante (LC exteriores paralelas):
o
dpe/dx>0 <–> U0 decrescente (LC exteriores divergentes):
dpe/dx<0 <–> U0 crescente (LC exteriores convergentes):
o
2004
 2u
0
2
y
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da camada limite
 Separação
da camada limite: inversão do escoamento
por acção de um gradiente de pressão adverso (pressão
cresce no sentido do escoamento) + acção viscosa
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da Camada limite
 Gradiente
de pressão nulo:
dpe/dx=0 <–> U0 constante (LC exteriores paralelas):
  2u 
 2   0
 y  y =d
y
u
Não pode ocorrer inversão
(separação) da camada limite
  2u 
 2  = 0
 y  y =0
Ponto de inflexão na parede
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da Camada limite
 Gradiente
de pressão favorável:
dpe/dx<0 <–> U0 crescente (LC exteriores convergentes):
  2u 
 2   0
 y  y =d
y
Não é possível haver
separação da CL
  2u 
 2   0
 y  y =0
2004
Perfil mantém a curvatura
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da Camada limite
 Gradiente
de pressão adverso:
dpe/dx>0 <–> U0 decrescente (LC exteriores divergentes):
  2u 
 2   0
 y  y =d
y
É possível haver
separação da CL
  2u 
 2   0
 y  y =0
P.I.
Perfil altera a curvatura
CL separada
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da Camada limite
 Resultante
das forças viscosas:
 2u
 2
y
anula-se com a velocidade
não pode provocar por si só estagnação do fluido
(menos ainda a inversão – separação - da CL)
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da Camada limite

Acção do gradiente longitudinal de pressão:
dpe
 0 (L.C. exteriores
dx
convergentes)
dpe
 0 (L.C. exteriores
divergentes)
dx
contraria acção viscosa
u
1 1 dpe
=
 ...
u r dx
perfis de velocidade x
mais cheios
reduz crescimento da CL
2004
Mecânica dos Fluidos II
reforça acção viscosa
perfis de velocidade
menos cheios
aumenta crescimento da CL
Prof. António Sarmento - DEM/IST
Separação da Camada limite

Acção do gradiente longitudinal de pressão:
perfis de velocidade
mais cheios
u
1 1 dpe
=
 ...
x
u r dx
perfis de velocidade
menos cheios
reduz crescimento da CL
aumenta crescimento da CL
Perfis mais cheios resistem melhor
a gradientes adversos de pressão
Escoamentos turbulentos (perfis mais cheios)
resistem melhor a gradientes adversos de pressão
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da Camada limite
Gradiente longitudinal adverso e intenso, não
provoca separação => não há forças viscosas
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da Camada limite

Na ausência de forças viscosas não há separação:
dV 1 dp
V
=
ds r ds
(ds deslocamento sobre a LC)
V=0 (ponto de estagnação)
não há inversão
do escoamento
2004
Mecânica dos Fluidos II
dp
=0
ds
Resultante da
Força de pressão
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II

Conceitos:
–
–
–
–
–
–
–
–
–
2004
Camada limite;
Espessura da camada limite;
Linha limite da CL;
Afastamento das linhas de corrente na CL;
Camada limite delgada;
Camada limite confinada e não-confinada;
Escoamentos de corte livre;
Esteira;
Equações para CL delgada.
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Separação da Camada limite

Conceitos:
– Separação da camada limite: condições para a ocorrência de
separação da camada limite;
– Gradientes de pressão nulos, favoráveis e adversos;
– Acção do gradiente de pressão sobre a evolução da C.L.
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
MECÂNICA DOS FLUIDOS II

Bibliografia:
– Sabersky – Fluid Flow: 8.1, 8.2
– White – Fluid Mechanics: 7.1, 7.3, 7.5
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST