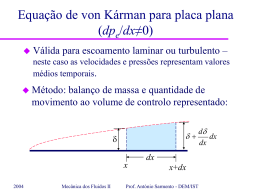
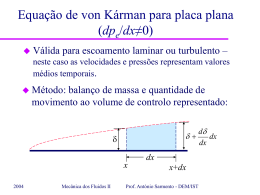
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Matéria:
– Solução de Blasius para CL laminar com gradiente de
pressão nulo;
– Parâmetros integrais: espessura de deslocamento e espessura
de quantidade de movimento;
– Equação de von Kárman: simplificação para gradiente de
pressão nulo.
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equações da camada limite laminar para placa
plana com dpe/dx=0
 Equações
de camada limite laminar 2D delgada
(d<<x) para placa plana:
u
u
 2u
u v
 2
x
y
y
u v

0
x y
 Condições
2004
de fronteira:
Mecânica dos Fluidos II
y=0
y=∞
u=v=0
u=U
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Solução:
U u
u  y x U  F F  
 F  
1,2
U
0,8
0,4
0
0
2004
2
0
1
2
3
4
5
6
7
8
Mecânica dos Fluidos II
0
0,3298
0,6298
0,8461

F0,9555
0,9916
0,999
6
4
0,999
U
1
y
 
x
0,3321
0,323
0,2668
0,1614
0,0642
0,0059
0,0024
8
0,0002
0,0001
Prof. António Sarmento - DEM/IST
10
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Solução:
U u
 F F  
y
x U
0
1
2
3
4
5
6
7
8
2004
0
0,3298
0,6298
0,8461
0,9555
0,9916
0,999
0,999
1
0,3321
0,323
0,2668
0,1614
0,0642
0,0059
0,0024
0,0002
0,0001
Mecânica dos Fluidos II
o Tensão de corte na parede
 u 
 0      U U F 0
 y  y 0
x
o Coeficiente de atrito
 0  2 F 0  0,664
c f  1 2 Ux
Re x
U
2

Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Solução:
U u
 F F  
y
x U
0
1
2
3
4
5
6
7
8
0
0,3298
0,6298
0,8461
0,9555
0,9916
0,999
0,999
1
0,3321
0,323
0,2668
0,1614
0,0642
0,0059
0,0024
0,0002
0,0001
o Força de resistência
L
D    0 dx 
o
1
U
U
F 0
2
L
o Coeficiente de resistência
D
1,328
CD 

1
Re L
U 2 L
2
Re L 
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
UL

Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Solução:
U u
 F F  
y
x U
0
1
2
3
4
5
6
7
8
2004
0
0,3298
0,6298
0,8461
0,9555
0,9916
0,999
0,999
1
0,3321
0,323
0,2668
0,1614
0,0642
0,0059
0,0024
0,0002
0,0001
Mecânica dos Fluidos II
o Espessura da CL
u y  d   0,99U
η=5
d
5
5


x
Ux 
Re x
o Tensão de corte em y=d
 d F 5

 1,8%
 0 F 0
Prof. António Sarmento - DEM/IST
Parâmetros integrais: Espessura de deslocamento

Espessura de deslocamento (dd ou d*):
1
dd 
U
d
1
dd 
U
 U  u dy
0
d
 U  u dy
Ud d  Ud   udy
0
0
Déficit de caudal devido à
redução de velocidade na CL.
Caudal para
fluido invíscido
U
d

Mecânica dos Fluidos II
Caudal real
 U  u dy
0
2004

Prof. António Sarmento - DEM/IST
Parâmetros integrais: espessura de deslocamento

Espessura de deslocamento (dd ou d*):
1
dd 
U
d
 U  u dy
0
1
dd 
U
 U  u dy
0
d
Ud d  Ud   udy
0
Déficit de caudal devido à
redução de velocidade na CL.
Caudal para
fluido invíscido
q  U d  d d 
2004

Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Caudal real
Parâmetros integrais: espessura de deslocamento

1
dd 
U
Espessura de deslocamento:
1
dd 
U
d
 U  u dy
0
2004
 U  u dy
0
d
1
d d  d   udy
U0
Afastamento inicial da LC
Desvio sofrido pela LC exterior
δ
q/U

δd
LC
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Solução de Blasius para a espessura de
deslocamento (Camada Limite Laminar)

Valor da solução de Blasius para a espessura de
deslocamento:
dd
1,72
Ux

com
Re x 
x
ou
dd
 0,344
d
δ
q/U
2004

Re x
dd
LC
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Parâmetros integrais: espessura de quantidade de
movimento

Espessura de quantidade de movimento (dm ou ):
1
dm  2
U
1
dm  2
U
d
 U  u udy

 U  u udy
0
0
d
d
d
d
0
0
0
0
U 2d m  U  udy   u 2 dy
d
2
2
u
dy

U
udy

U
dm


2
2
d  d d  d m 
u
dy

U

 U d  d d 
0
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Parâmetros integrais: espessura de quantidade de
movimento

Caudal de quantidade de movimento através duma
secção da CL:
d
qqmx   u 2 dy  U 2d  U 2d d  U 2d m
0
U Ud 
U Ud d 
Caudal de q.m.
com perfil
uniforme
Redução devido
ao déficit de
caudal
2004
Mecânica dos Fluidos II
U Ud m 
Redução devido
ao déficit de
q.m. na C.L.
Prof. António Sarmento - DEM/IST
Parâmetros integrais: espessura de quantidade de
movimento

Balanço de quantidade de movimento longitudinal
entre o bordo de ataque e a secção afastada de x:
 
D  qqmx
x 0
 
 qqmx
x x
U 2 d  d d 
U 2d m
d-dd
δ
U 2 d  d d  dm
dd
LC
x
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Solução de Blasius (Camada Limite Laminar)
para espessura da quantidade de movimento

Valor da solução de Blasius para a espessura de
quantidade de movimento:
dm
0,664

x
Re x
ou
com
Re x 
dm
 0.133
d
dd
Factor de forma:
 2,59
dm
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Ux

Equação de von Kárman para placa plana
(dpe/dx≠0)
 Válida
para escoamento laminar ou turbulento –
neste caso as velocidades e pressões representam valores
médios temporais.

Método: balanço de massa e quantidade de
movimento ao volume de controlo representado:
dd
d
dx
dx
d
dx
x
2004
Mecânica dos Fluidos II
x+dx
Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
d
M VC   m x  m d  m x  dx
 Balanço de massa:
dt
m d
Esc. estacionário
m x
m x  dx
dx
o Caudal
o Caudal
2004
m x :
d


m x    udy
0
x
m x  dx : m x  dx
d

d 
  udydx

dx  0

d
d


d 
   udy    udydx
0
 x dx  0

Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
 Balanço
de massa:
d

d 
m d    udydx
dx  0

m d
m x
m x  dx
dx
o Caudal de quantidade de movimento segundo x através y=δ:
qqm x
2004
d


d
  udy
 Um d  U

dx  0

Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
 Balanço
de q. movimento segundo x:
dKxVC
dt


 qqmx x  qqmxd  qqmx x  dx  FxVC
qqmx d
esc. estacionário
qqmx x qqmx xdx
o Diferença qqmx xdx  qqmx x :
2004
Mecânica dos Fluidos II
d

d 
2

   u dy dx
dx  0

Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
 Balanço
de q. movimento segundo x:


FxVC  qqmx x dx  qqmx x  qqmxd
d

d 
2
  u dy dx

dx  0

d

d 
U   udy
dx  0

qqmx d
qqmx x qqmx xdx
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
 Forças
FxVC
segundo x:
1 

 pd   p  dpd  dd    p  dpdd   0 dx
2 

FxVC
dp 

  0  d
dx
dx 

dp e
dU
  U
dx
dx
p+1/2dp
p
p+dp
τ0
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
 Resultado:
d
d

dU
 0    U  u udy 
 U  u dy

x 0
dx 0
 Introduzindo dd e δm:


d
dU
2
0 
U d m  Ud d
dx
dx
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Equação de von Kárman para
placa plana (dpe/dx≠0)
 Caso
em que dpe/dx=0 (dU/dx=0):
dd m
 0  U
dx
2
0
dd m
cf 
2
1
dx
2
U
2
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Conceitos:
– Solução de Blasius para CL laminar com gradiente de
pressão nulo;
– Número de Reynolds local;
– Número de Reynolds global;
– Espessura de deslocamento;
– Espessura de quantidade de movimento;
– Equação de von Kárman: simplificação para gradiente de
pressão nulo.
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Bibliografia:
– Sabersky – Fluid Flow: 8.3, 8.4, 8.6 e 8.7
– White – Fluid Mechanics: 7.3, 7.4
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST