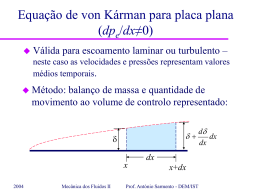
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0
 Equações
de camada limite laminar 2D delgada
(d<<x) para placa plana:
u
u
 2u
u v
 2
x
y
y
u v

0
x y
 Condições
2004
de fronteira:
Mecânica dos Fluidos II
y=0
y=∞
u=v=0
u=U
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0
 Hipótese
de Blasius: u  f   com   Ayn
U
x
A introdução de η corresponde a reconhecer que o perfil de
velocidades adimensional está estabilizado.
A e n são parâmetros a determinar.
 Nota:
2004
 A 
e
 n 
y x
y
Mecânica dos Fluidos II

nA
n
  n 1 y   
x
x
x
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Procedimento:
o Utilizar a função corrente:

u
y

v
x
o Substituir u/U=f(η) e v    x na equação da CL,
escolher n de modo a que a equação resultante não
dependa de x e A de modo a simplificar a equação.
o Nota:
d 

d y

xn
xn
u
 Uf  
y
A
A
xn
 U
A
 f  d
F  
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0
n
x
 De:   U
F  
A

resulta:

 UF  
o u
y
u
nU

F  
o
x
x
u UA
 n F  
o
y x
 2u UA2
o
 2 n F  
2
y
x
o
2004



U
v
  nx n 1 F    nx n 1 F  
x
A
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0
 Obtém-se:
u
u
 2u
u v
 2
x
y
y
Unx2 n1
F  
FF   0
2
A
o Tomando n=1/2 e A  U  simplifica a equação para:
U
2F    F  F    0 com   y
x
 Condições
ux,0  0
vx,0  0
ux,   U
2004
fronteira:
UF 0  0
F   F 0  0
UF   U
Mecânica dos Fluidos II
F 0  0
F 0  0
F   1
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Solução:
U u
u  y x U  F F  
 F  
1,2
U
0,8
0,4
0
0
2004
2
0
1
2
3
4
5
6
7
8
Mecânica dos Fluidos II
0
0,3298
0,6298
0,8461

F0,9555
0,9916
0,999
6
4
0,999
U
1
y
 
x
0,3321
0,323
0,2668
0,1614
0,0642
0,0059
0,0024
8
0,0002
0,0001
Prof. António Sarmento - DEM/IST
10
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Solução:
U u
 F F  
y
x U
0
1
2
3
4
5
6
7
8
2004
0
0,3298
0,6298
0,8461
0,9555
0,9916
0,999
0,999
1
0,3321
0,323
0,2668
0,1614
0,0642
0,0059
0,0024
0,0002
0,0001
Mecânica dos Fluidos II
o Tensão de corte na parede
 u 
 0      U U F 0
 y  y 0
x
o Coeficiente de atrito
 0  2 F 0  0,664
c f  1 2 Ux
Re x
U
2

Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Solução:
U u
 F F  
y
x U
0
1
2
3
4
5
6
7
8
0
0,3298
0,6298
0,8461
0,9555
0,9916
0,999
0,999
1
0,3321
0,323
0,2668
0,1614
0,0642
0,0059
0,0024
0,0002
0,0001
o Força de resistência
L
D    0 dx 
o
1
U
U
F 0
2
L
o Coeficiente de resistência
D
1,328
CD 

1
Re L
U 2 L
2
Re L 
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
UL

Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Solução:
U u
 F F  
y
x U
0
1
2
3
4
5
6
7
8
2004
0
0,3298
0,6298
0,8461
0,9555
0,9916
0,999
0,999
1
0,3321
0,323
0,2668
0,1614
0,0642
0,0059
0,0024
0,0002
0,0001
Mecânica dos Fluidos II
o Espessura da CL
u y  d   0,99U
η=5
d
5
5


x
Ux 
Re x
o Tensão de corte em y=d
 d F 5

 1,8%
 0 F 0
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Espessura de deslocamento:
1
dd 
U
d
1
*
d  dd 
U
 U  u dy
0
d
 U  u dy
Ud d  Ud   udy
0
0
Déficit de caudal devido à
redução de velocidade na CL.
Caudal para
fluido invíscido
U
d

Mecânica dos Fluidos II
Caudal real
 U  u dy
0
2004

Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Espessura de deslocamento:
1
dd 
U
d
 U  u dy
0
1
dd 
U

 U  u dy
0
d
Ud d  Ud   udy
0
Déficit de caudal devido à
redução de velocidade na CL.
Caudal para
fluido invíscido
q  U d  d d 
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Caudal real
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

1
dd 
U
Espessura de deslocamento:
1
dd 
U
d
 U  u dy
0
2004
 U  u dy
0
d
1
d d  d   udy
U0
Afastamento inicial da LC
Desvio sofrido pela LC exterior
δ
q/U

δd
LC
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Valor da solução de Blasius para a espessura de
deslocamento:
dd
1,72
Ux

com
Re x 
x
ou
dd
 0,344
d
δ
q/U
2004

Re x
dd
LC
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Espessura de quantidade de movimento:
1
dm  2
U
1
  dm  2
U
d
 U  u udy

 U  u udy
0
0
d
d
d
d
0
0
0
0
U 2d m  U  udy   u 2 dy
d
2
2
u
dy

U
udy

U
dm


2
2
d  d d  d m 
u
dy

U

 U d  d d 
0
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Caudal de quantidade de movimento através duma
secção da CL:
d
qqmx   u 2 dy  U 2d  U 2d d  U 2d m
0
U Ud 
U Ud d 
Caudal de q.m.
com perfil
uniforme
Redução devido
ao déficit de
caudal
2004
Mecânica dos Fluidos II
U Ud m 
Redução devido
ao déficit de
q.m. na C.L.
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Balanço de quantidade de movimento longitudinal
entre o bordo de ataque e a secção afastada de x:
 
D  qqmx
x 0
 
 qqmx
x x
U 2 d  d d 
U 2d m
d-dd
δ
U 2 d  d d  dm
dd
LC
x
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Valor da solução de Blasius para a espessura de
quantidade de movimento:
dm
0,664

x
Re x
ou
2004
com
Re x 
dm
 0.133
d
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Ux

Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Conceitos:
– Solução de Blasius para CL laminar com gradiente de
pressão nulo;
– Número de Reynolds local;
– Número de Reynolds global;
*
– Espessura de deslocamento ; d  d d
– Espessura de quantidade de movimento:   d m
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Solução de Blasius para a equação da camada
limite laminar para placa plana com dpe/dx=0

Bibliografia:
– Sabersky – Fluid Flow: 8.3, 8.4
– White – Fluid Mechanics: 7.4 (sem método de Thwaites)
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Problema
Placa de espessura desprezável, muito larga, e comprimento L=2 m.
Escoamento de ar (=1,2 kg/m3, =1,810-5 Pa.s) não-perturbado
paralelo com U=2 m/s. Gradiente longitudinal de pressão nulo sobre a
placa. Transição para regime turbulento ocorre para Rex=106.
=1,2 kg/m3,
=1,810-5 Pa.s
(Rex)c =106.
U=2m/s
dpe dx  0
L=2m
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Problema
=1,2 kg/m3,
=1,810-5 Pa.s
(Rex)c =106.
dpe dx  0
U=2m/s
L=2m
a) Determine a espessura da camada limite d nas secções S1 e S2,
respectivamente às distâncias x1=0,75 m e x2=1,5 m.

5
1
,
8

10
1,2
6
Determinação de xc: xc  Re x c  10
 7,5m
U
2
CL Laminar em x1 e x2 pelo que se aplica a solução de Blasius:
d
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
5

x Re x
Problema
a) Determine a espessura da camada limite d nas secções S1 e S2,
respectivamente às distâncias x1=0,75 m e x2=1,5 m.
CL Laminar em x1 e x2 pelo que se aplica a solução de Blasius:
d
5

x Re x
2  0,75
5


10
1,5  105
x1  0,75m
Re x1
x2  1,5m
Re x 2  2 105
2004
Mecânica dos Fluidos II
d1 
0,75 5
5
 0,0119m
10
d 2  0,0168m
Prof. António Sarmento - DEM/IST
Problema
=1,2 kg/m3,
=1,810-5 Pa.s
(Rex)c =106.
U=2m/s
dpe dx  0
L=2m
b) Verifique que se trata de uma camada limite delgada.
R: É delgada se d/x<<1:
Porque motivo d/x em 2 é
menor que em 1?
2004
Mecânica dos Fluidos II
0,0119
d 
 0,0159
  
0,75
 x 1
0,0168
d 

 0,0112
 
1,5
 x 2
Prof. António Sarmento - DEM/IST
Problema
=1,2 kg/m3,
=1,810-5 Pa.s
(Rex)c =106.
dpe dx  0
U=2m/s
Linha de corrente
d
y1=?
x1=0,75m
L=2m
x2=1,5m
d) Calcule a ordenada y1 em x1 da linha de corrente que passa pelo ponto
definido pelas coordenadas x2=1,5 e y2=d.
R: entre a linha de corrente e a placa passa o mesmo caudal nas duas secções
Caudal que atravessa uma secção transversal da CL: q  U d  d d 
Caudal que atravessa a secção 2: q2  U d  d d 2
y1  d 2  d d 2  d d1
y1
d1
y1
0
0
d1
Caudal que atravessa a secção 1: q1   udy   udy   udy  U d  d d 1 U  y1  d1 
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Problema
=1,2 kg/m3,
=1,810-5 Pa.s
(Rex)c =106.
dpe dx  0
U=2m/s
Linha de corrente
y1=?
x1=0,75m
L=2m
d
x2=1,5m
d) Calcule a ordenada y1 em x1 da linha de corrente que passa pelo ponto
definido pelas coordenadas x2=1,5 e y2=d.
R: entre a linha de corrente e a placa passa o mesmo caudal nas duas secções
y1  d 2  d d 2  d d1
0,0168m 0,011m 0,078m
2004
Numa CL Laminar: d d  0,344d
y1=0,0136m
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
d m1  0,133d1  0,00158m
Problema
=1,2 kg/m3,
=1,810-5 Pa.s
(Rex)c =106.
dpe dx  0
U=2m/s
L=2m
e) Estime a força por unidade de largura que se exerce entre as secções S1 e S2.
R: Não há outras forças aplicadas excepto a resistência imposta pela placa
A força aplicada entre o bordo de ataque e a secção x é:
Para uma CL laminar:
d m2  0,133d 2  0,00223m
d m1  0,133d1  0,00158m
d m  0,133d
D0, x  U 2 d m x
Resistência até à secção 2: D0,2=0,0107N/m
Resistência até à secção 1: D0,1=0,0076N/m
Resistência entre 1 e 2: D1,2=D0,2-D0,1=0,0031N/m
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST
Problema
=1,2 kg/m3,
=1,810-5 Pa.s
(Rex)c =106.
U=2m/s
dpe dx  0
L=2m
f) A seguinte afirmação é verdadeira ou falsa: ”Nas condições do
enunciado, se a placa fosse suficientemente comprida (L
), a camada limite acabaria por se separar?
É falsa: as forças de atrito reduzem-se com a velocidade
sobre a placa, nunca podem parar o fluido
2004
Mecânica dos Fluidos II
Prof. António Sarmento - DEM/IST