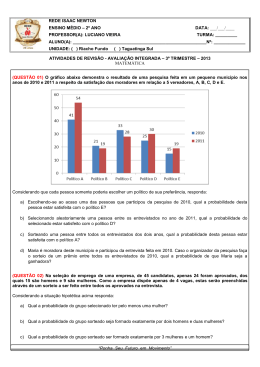
Cilindros
A junção de dois círculos localizados em dois planos paralelos se denomina cilindro
Bases: Círculos em planos paralelos
Altura: Distância entre os círculos
Eixo: Reta que passa pelo centro das bases
Geratriz: Segmentos paralelos ao eixo e com extremidade nas circunferências

Secções de um cilindro
Secção Transversal
Cilindro Circular Reto  g = h




Secção Meridiana
Cilindro Oblíquo
Cilindro Equilátero  Secção meridiana é
um quadrado (h = 2r)
Área da base  Ab = π r***2
Área lateral  Al = 2 π r h
Área total  At = Ab + Al = 2 π r (r + h)
Volume  V = Ab h = π r***2 h
Cones
Ligando-se todos os pontos de um círculo a um ponto V fora do plano do circulo obtém - se um cone

Secções de um cone
Secção transversal
Secção meridiana
Cone Reto  Girando um triângulo
retângulo em torno de um de seus
catetos obtém - se esse cone
Cone Oblíquo  projeção do
vértice não coincide com o
centro da base




Área da base  Ab = π r***2
Área lateral  Al = π r g
Área total  At = Ab + Al
Volume  V = 1/3 Ab h

Tronco de cone
Cone Equilátero  g = 2r