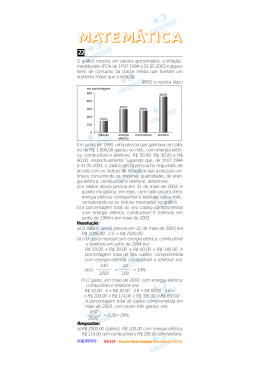
Questão 22
O gráfico mostra, em valores aproximados, a
inflação medida pelo IPCA de 1º.07.1994 a
31.05.2003 e alguns itens de consumo da
classe média que tiveram um aumento maior
que a inflação.
(IBGE e revista Veja.)
a) O salário da pessoa em 31 de maio de 2003,
reajustado de acordo com a inflação, foi
1 000(1 + 150%) = 2 500 reais, enquanto os gastos com energia elétrica, combustível e telefone
foram 50(1 + 300%) = 200 reais, 30(1 + 280%) =
= 114 reais e 60(1 + 460%) = 336 reais, respectivamente.
b) A porcentagem total do salário da pessoa comprometida com energia elétrica, combustível e telefone em junho de 1994 e em maio de 2003 fo50 + 30 + 60
ram, respectivamente,
= 14% e
1 000
200 + 114 + 336
= 26% .
2 500
Questão 23
Em junho de 1994, uma pessoa que ganhava
um salário de R$ 1.000,00 gastou no mês,
com energia elétrica, combustível e telefone,
R$ 50,00, R$ 30,00 e R$ 60,00, respectivamente. Supondo que, de 1º.07.1994 a
31.05.2003, o salário dessa pessoa foi reajustado de acordo com os índices de inflação e
que a pessoa continuou consumindo as mesmas quantidades de energia elétrica, combustível e telefone, determine:
a) o salário dessa pessoa em 31 de maio de
2003, e quanto ela gastou, em reais, com cada
um dos itens energia elétrica, combustível e
telefone nesse mês, considerando-se os índices mostrados no gráfico.
b) a porcentagem total do seu salário comprometida com energia elétrica, combustível e
telefone em junho de 1994 e em maio de
2003.
Resposta
Do gráfico, vemos que a inflação foi de 150% enquanto os gastos com energia elétrica, combustível e telefone aumentaram 300%, 280% e 460%,
respectivamente, durante o período de 1º/07/1994
a 31/05/2003.
Numa festa de aniversário infantil, 5 crianças comeram um alimento contaminado com
uma bactéria. Sabe-se que, uma vez em contato com essa bactéria, a probabilidade de
que a criança manifeste problemas intestinais
é de 2/3.
⎛ n⎞
n!
Sabendo que ⎜ ⎟ =
, determine:
k!( n − k)!
⎝ k⎠
⎛5⎞
a) ⎜ ⎟ e a probabilidade de manifestação de
⎝2⎠
problemas intestinais em exatamente duas
crianças.
⎛5⎞ ⎛5⎞
b) ⎜ ⎟ , ⎜ ⎟ e a probabilidade de manifestação
⎝0⎠ ⎝1⎠
de problemas intestinais no máximo em uma
criança.
Resposta
A probabilidade de que exatamente k crianças,
0 ≤ k ≤ 5 , manifestem problemas intestinais é:
⎛5 ⎞ ⎛ 2
⎜ ⎟ ⋅⎜
⎝k ⎠ ⎝ 3
⎞
⎟
⎠
k
2⎞
⎛
⋅ ⎜1 − ⎟
⎝
3⎠
5 −k
⎛5 ⎞ 2 k
=⎜ ⎟ ⋅ 5
⎝k ⎠ 3
Assim:
⎛5 ⎞
5 ⋅4
a) ⎜ ⎟ =
= 10 e a probabilidade pedida é
⎝2 ⎠
2
⎛5 ⎞ 2 2
40
.
⎜ ⎟ ⋅ 5 =
⎝2 ⎠ 3
243
matemática 2
⎛5 ⎞
⎛5 ⎞
b) ⎜ ⎟ = 1, ⎜ ⎟ = 5 e a probabilidade é
⎝0 ⎠
⎝1 ⎠
⎛5 ⎞ 2 0
⎛ 5 ⎞ 21
11
.
⎜ ⎟ ⋅ 5 +⎜ ⎟ ⋅ 5 =
⎝0 ⎠ 3
⎝1 ⎠ 3
243
números positivos, o único valor de x diferente de
5 cm é
15 − 141
cm.
2
Questão 25
Questão 24
A expressão V(x) = x(16 − 2x)(24 − 2x) representa o volume em cm 3 de uma caixa na forma de um paralelepípedo retângulo reto, em
que x é a altura e os lados da base são 16 − 2x
e 24 − 2x.
a) Se nenhuma das arestas da caixa pode ser
menor que 1 cm, determine os valores possíveis da variável x.
b) Quando x = 5 cm, o volume da caixa é
420 cm 3 . Investigue se existem outros valores de x para os quais o volume é 420 cm 3 .
Em caso afirmativo, dê esses valores.
Um recipiente, na forma de um cilindro circular reto de raio R e altura 32 cm, está até à
metade com água (figura 1). Outro recipiente,
na forma de um cone circular reto, contém
uma substância química que forma um cone
de altura 27 cm e raio r (figura 2).
Resposta
a) Como nenhuma
menor que 1 cm,
x ≥1
x
16 − 2x ≥ 1 ⇔ x
24 − 2x ≥ 1
x
das arestas da caixa pode ser
≥1
≤ 7,5 ⇔ 1 ≤ x ≤ 7,5
≤ 11,5
b) V(x) = 420 ⇔ x ⋅ (16 − 2x) ⋅ (24 − 2x) = 420 ⇔
⇔ x ⋅ 2 ⋅ 2 ⋅ (8 − x) ⋅ (12 − x) = 420 ⇔
⇔ x 3 − 20x 2 + 96x − 105 = 0 ( ∗)
Sendo x = 5 uma raiz da equação ( ∗), pelo dispositivo prático de Briot-Ruffini,
5
Assim x
3
−20
96
−105
1
−15
21
0
− 20x
⇔ (x − 5) ⋅ (x
x =
1
2
2
+ 96x − 105 = 0 ⇔
− 15x + 21) = 0 ⇔ x = 5 ou
15 + 141
= 7,5 +
2
141
ou
2
15 − 141
141
.
= 7,5 −
2
2
121
141
144
Uma vez que
<
<
⇔
2
2
2
x =
141
141
< 6, 13 < 7,5 +
< 13,5 e
2
2
141
1 < 7,5 −
< 1,5 . Sendo as arestas da caixa
2
⇔ 5,5 <
a) Sabendo que R = (3/2)r, determine o volume da água no cilindro e o volume da substância química no cone, em função de r. (Para
facilitar os cálculos, use a aproximação π = 3.)
b) A substância química do cone é despejada
no cilindro, formando uma mistura homogênea (figura 3). Determine a concentração
(porcentagem) da substância química na mistura e a altura h atingida pela mistura no cilindro.
Resposta
a) Sendo a medida r em cm e usando a aproximação dada π ≅ 3, o volume da água no cilindro é
2
32
⎛3 ⎞
igual a π ⋅ ⎜ r ⎟ ⋅
= 36 πr 2 ≅ 108 r 2 cm 3 e o
⎝2 ⎠
2
volume da substância química no cone é igual a
1
πr 2 ⋅ 27 = 9 πr 2 ≅ 27r 2 cm 3 .
3
b) A porcentagem volumétrica da substância quí9 πr 2
mica na mistura é igual a
=
2
9 πr + 36 πr 2
= 0,2 = 20% e a altura h atingida pela mistura no
2
⎛3 ⎞
cilindro é tal que π ⋅ ⎜ r ⎟ ⋅ h = 45 πr 2 ⇔
⎝2 ⎠
⇔ h = 20 cm.