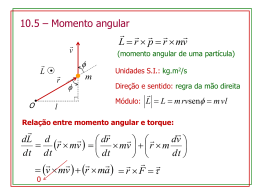
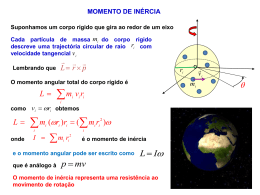
Leis de Newton
• Ação e reação…
• Inércia…
• Força… Variação da quantidade de movimento


dP
F 
dt
MOMENTUM…
Quantidade de movimento


P  mv
Momento linear
Leis de Newton para rotações
• Ação e reação…
• Inércia…
• Força… Variação da quantidade de movimento
• Torque… Variação da quantidade de movimento angular
 
  r F

kˆ

O

r

F

F

F //
  r  F  sen rF
 

F  F  F//
Quantidade de movimento angular ou Momento angular
  
L  r P
L  r  m  v  senrP


dL
 
dt
Leis de Newton para rotações

v
•Para uma partícula…


r
L  r  P  sen rP
L  rP
L  r mv
L  I 
L  r  m   r  m  r  w
2
Para um sistema de partículas…
L   ri  Pi
i
L   ri  mi  vi
i
L   ri  mi  i  ri   mi  ri  
2
i
i
L  I 
Rotação
Translação
P= mv
momento linear
F= ma
força
m
massa

dP 
 FR
dt
L= I
momento angular
= I
torque
I = mR2
momento de inércia

dL 
R
dt
Leis de Conservação
Momento Angular de um sistema de partículas
 N
L   Li

dL
i 1


dt
Momento Linear de um sistema de partículas

dP 
F
dt
 N 
P   pi
i 1
Conservação da Energia de um sistema de partículas
E 
 T
N
i 1
i
 U iext  U int

- Conservação do momento angular
A mergulhadora da figura ao lado parte com um
momento angular total L devido ao torque
externo inicial

  
dL
  ri  Fi  R
dt i
Mas, no referencial do CM (acelerado
neste caso)

L


R

Mg
dL
 
 
  ri   Fi   mi ri   g  0
dt
i
i


0


dL

 0  L  const. e o CM segue o movimento
parabólico !
dt
- Conservação do momento angular
No sistema homem - halteres só há forças internas e, portanto,
L( z )  I  const.
i
Ii

I ii  I f  f
If
f
- Exemplo
Dados
I bic 1,2 kg. m 2 ; I tot  6,8 kg. m 2 e i  3,9rot / s
Queremos calcular a velocidade
angular final do sistema após o menino
inverter o eixo de rotação da roda de
bicicleta (ver figura)
Momento angular inicial do sistema
roda de bicicleta – menino (+ banco)
Li  Lbic  I bici
Menino inverte o eixo de rotação da roda de bicicleta
Lbic   Li
- Exemplo
Momento angular final do sistema
L f  Lbic  Lmen  Lmen  Li
Conservação do momento angular pois só
há forças internas no sistema
L f  Li  Lmen  Li  Li
 Lmen  2 Li
I tot  2 Ii
2 Ii

1,4 rot / s
I tot
- Precessão do momento angular

Módulo do torque da força peso
  Mgr sin 
Lei fundamental da dinâmica das rotações
 
L   t
L  Mgr sin  t
Da figura temos

L  L sin    I sin  
- Precessão do momento angular

Mgr sin  t  I sin  
Velocidade angular de precessão
d Mgr


dt
I

- Precessão do momento angular
Como a Terra é um esferóide a Lua e o Sol provocam forças
como as mostradas abaixo e em 13000 anos...
Exercício
O gráfico mostra o torque que atua sobre um disco inicialmente
estacionário que pode girar em torno de seu centro como um
carrossel. Qual é o momento angular do disco nos tempos (a) t = 7,0
s e (b) t= 20s?
 ( N  m)
4
2
4
-2
8
12
16
20
t (s)
Exercício
O gráfico mostra o Momento Angular de um disco girando em torno
de seu centro como um carrossel. Qual é o torque externo aplicado
nos intervalos (a) 0 a 2 segundos; (b) 9 a 12 segundos e (c) 17 a
20s?
L (kg  m2 / s)
4
2
4
-2
8
12
16
20
t (s)