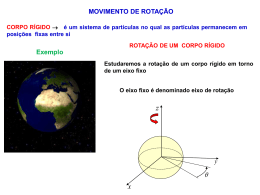
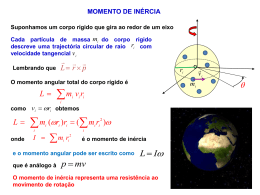
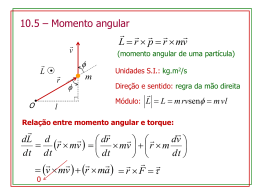
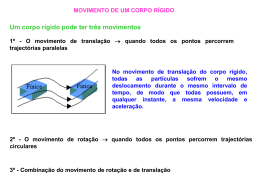
MOVIMENTO DE ROTAÇÃO
CORPO RÍGIDO  é um sistema de partículas no qual as partículas permanecem em
posições fixas entre si
ROTAÇÃO DE UM CORPO RÍGIDO
Exemplo
Estudaremos a rotação de um corpo rígido em torno
de um eixo fixo
O eixo fixo é denominado eixo de rotação
z
y

x
O sentido da rotação é dado pela regra da mão direita
z
positivo
negativo

MOMENTO DA FORÇA ( ou TORQUE)
Quando empurramos uma porta, estamos aplicando uma força sobre a porta
 como consequência a porta vai girar em torno dum eixo fixo que passa
pelas dobradiças.
A tendência da força de rodar o corpo em torno de um
eixo é medida por uma grandeza vectorial denominada
momento da força (ou torque)
r
O momento da força é a causa dos movimentos
rotacionais
É análogo a força que causa variações no movimento
translacional
Definimos o momento da força por
  
M  rF
O módulo do momento da força é

M

F
M  rF sin 
Corresponde ao produto da distância até o ponto de aplicação da
força e a componente perpendicular da força.

r

APLICAÇÃO DUMA FORÇA EM PONTOS DIFERENTES NUMA PORTA
Quando fechar uma porta, experimente fechá-la, empurrando-a no centro da porta
(Figura a) e depois, aplicando a mesma força, empurre a porta na extremidade (Figura
b).
M  rF sin 
A porta é fechada mais facilmente quando a força é aplicada na
extremidade da porta
O que é uma alavanca? É uma barra rígida apoiada (ponto de apoio O)
utilizada para facilitar o deslocamento de um corpo pesado.
A distância do ponto de apoio O, por onde passa o eixo de rotação, à linha de
acção da força F, é denominada braço de alavanca, (L)
Arquimedes disse: “Dê-me uma
alavanca que moverei o mundo”
M  rF sin 

M  (r sin ) F  LF
O MOMENTO ANGULAR
Definimos inicialmente
o momento angular

momento linear p .
  
L r p

é o momento angular instantâneo L

L
de uma partícula com
em
  
L r p
relação à origem O
Note que a partícula não precisa estar girando em
torno de O para ter momento angular em relação a este
ponto

r
m

p
Podemos obter para o movimento rotacional uma
lei de movimento semelhante à Segunda Lei de
Newton

Derivando o momento angular
L
em relação ao tempo:



dL d  
dr   dp
 (r  p) 
 p  r
dt dt
dt
dt
=0
mas


 dp
f 
dt


dL  
 r f  M
dt
ou

 dL
M
dt

 dp
f 
dt
análogo à segunda lei de newton
A relação acima é válida também para um sistema
de partículas onde o momento angular é a soma
vectorial dos momentos angulares de cada partícula
 em relação ao mesmo ponto fixo O
A mesma relação é válida para um corpo
rígido, em rotação em torno de um ponto O.

 dL
M
dt
A soma dos momentos das forças internos são nulos
e

M
corresponde à um momento da força externo resultante
O

MOMENTO DE INÉRCIA
Suponhamos um corpo rígido que gira ao redor de um eixo
Cada partícula de massa mi do corpo rígido
descreve uma trajectória circular de raio ri com
velocidade tangencial v i
Lembrando que
  
L r p
ri
O momento angular total do corpo rígido é
L
mi
m v r
i
i i
i
como vi  ri obtemos
L
2
m
(

r
)
r

(
m
r
 i i i  i i )
i
onde
I 
m r
i
i
i
2
é o momento de inércia
e o momento angular pode ser escrito como
que é análogo à
p  mv
o
vi
L  I
O momento de inércia representa uma resistência ao
movimento de rotação

CONSERVAÇÃO DO MOMENTO ANGULAR
Quando

 dL  

M
 r  f  0  L  constante
dt


se
f  0 ou
r 0

M 0
ou

L  constante


Li  L f
Análogo ao que acontece com o momento linear
 
pi  p f
PARA QUE O MOMENTO DA FORÇA SEJA NULO NÃO É PRECISO QUE A FORÇA SEJA
NULA, QUANDO A FORÇA É COLINEAR COM O VECTOR POSIÇÃO TEREMOS TAMBÉM

M 0
Exemplo:
FORÇAS CENTRAIS, que são forças da forma
 

F (r )  f (r ) u
Neste caso:

 dL 

M
 r  f (r )u  0
dt

 L  constante
EXEMPLO 1 DA CONSERVAÇÃO DO MOMENTO ANGULAR
No sistema homem - halteres só há forças internas e, portanto:
L  I  constante

f I f
i I i
Com a aproximação dos halteres (
I i i  I f  f
If
<
Ii
) a velocidade angular do sistema aumenta
EXEMPLO 2: CONSERVAÇÃO DO MOMENTO ANGULAR
Queremos calcular a velocidade angular final do sistema após o menino
inverter o eixo de rotação da roda de bicicleta
Dados
Ibic  1, 2 kg.m2 ; Itot  6,8 kg.m2 e i  3,9 rot/s
Momento angular inicial do sistema
bicicleta-menino (+ banco)
roda de
Li  Lbic  I bici
Agora o menino inverte o eixo de rotação da
roda de bicicleta
Lbic   Li
EXEMPLO 2 (cont): CONSERVAÇÃO DO MOMENTO ANGULAR
Momento angular final do sistema:
L f  Lbic  Lmen  Lmen  Li
Há conservação do momento angular 
uma vez que só há forças internas no
sistema
L f  Li  Lmen  Li  Li
 Lmen  2 Li
I tot  2I bici
2 I bic i
 
 1,4
I tot
rot/s
QUANDO O MOMENTO ANGULAR VARIA COM O TEMPO
dL d
d
 ( I )  I
 I
dt dt
dt
ou


M  I
que é semelhante à equação de Newton


F  ma