Análise de Sistemas LTI no Domínio da Transformada
1. Introdução.
2. Resposta em Frequência de Sistemas LTI.
3. Equação Diferença de Sistemas LTI.
4. Análise da Função Sistemas no Domínio da Frequência.
5. Relação entre Módulo e Fase.
6. Sistema Passa-tudo (all-pass).
7. Sistemas de Fase Mínima.
8. Representação da Equação Diferença por Diagrama de Blocos
9. Estruturas Básicas para Sistemas IIR e FIR.
1
Introdução
Um sistema LTI pode ser completamente caracterizado no domínio do
tempo pela sua resposta ao impulso h[n]. A saída y[n] devido a uma
dada entrada x[n] é especificada através da convolução soma
y[n]  x[n]  h[n] 

 x[k ]h[n  k ]
k  
Usando a propriedade da convolução pode-se representar transformada
Z da resposta ao impulso por:
Y(z) = H(z)X(z)
com uma ROC apropriada.
A resposta em frequência de um sistema LTI H(e jω ) é definida como a
transformada de Fourier da resposta ao impulso h[n]. A transformada
de Fourier da entrada e da saída do sistema é estão relacionadas por:
Y(e jω )  H(e jω )X(ejω )
| Y(e jω ) || H(e jω ) | X(ejω )
módulo
fase[Y(e jω )]  fase[ H(e jω )]  fase[ X(ejω )]
2
Filtros Ideais
Filtro passa-baixa
Resposta em frequência
1,
H lp (e )  
 0,
j
|  |  c
 c |  | 
Filtro passa-alta
Resposta em frequência
0,
H ap (e )  
 1,
j
|  | c
c |  | 
Resposta ao impulso
sen( c n)
hlp [n] 
,   n  
n
Resposta ao impulso
hlp [n]   [n]  hlp [n]   [n] 
sen(c n)
n
Um filtro passa baixa ideal é não causal e sua resposta se estende de
- a +. Portanto não é possível computar a saída de um filtro
passa baixa ideal recursivamente ou não recursivamente, isto é, não é
computacionalmente realizável.
A resposta em fase de um filtro passa baixa ideal é zero.
3
Fase e Retardo de Grupo
Para entender os efeitos da fase de um sistema linear, considere um
sistema com retardo ideal e a sua resposta em frequência.
hid [n]   [n  nd ];
Hid(e jω )  e jnd ;
| Hid(e jω ) | 1;
fase[Hid(e jω )]  ωnd , |  | 
com periodicidade 2 e nd inteiro.
Exemplo: filtro passa-baixa ideal
 jnd

e
,
|  |  c
j
H lp (e )  
 0,  c |  | 
sen( c (n  nd )
hlp [n] 
,   n  
(n  nd )
retardo de grupo indica o grau de (não) linearidade da fase
 ( )  grd [ H (e j )]  
d
{arg[ H (e j )]}
d
4
Retardo de Grupo
 ( )  grd [ H (e j )]  
d

arg[ H (e j )]
d
• Se () é constante, então fase é linear ou zero.
• O desvio do valor constante indica não linearidade.
Espectro de fase
Retardo de grupo
5
Resposta para Sistemas Caracterizado por
Equações Diferenças com Coeficientes Constantes
Considere a classe de sistemas cuja relação entre a entrada e a saída
satisfazem a equação:
N
M
 a yn  k    b xn  k 
K o
k
k o
k
Aplicando a transformada Z em ambos os lados, tem-se:
M
N
a z
k o
k
k
M
Y ( z )   bk z k X z 
k o
H z  
Y z 

X z 
k
b
z
k
k o
N
a z
k o
k
k
Explicitando as raízes
M
H ( z) 
b0
a0
1
(
1

c
z
 k )
zeros : c1, c2 ,...,cM .
1
(
1

d
z
 k )
p' olos: d1 , d2 ,...,d N .
k 1
N
k 1
6
Exemplo 1: Dado H(z) para um sistema determine a sua equação
diferença.
(1  z 1 ) 2
H ( z) 
1
3
(1  z 1 )(1  z 1 )
2
4
Y( z )
1  2 z 1  z 2
H( z ) 

1 1 3 2
X( z )
1 z  z
4
8
1
3
1
Y ( z )  Y ( z )z  Y ( z )z 2  X ( z )  2 X ( z )z 1  X ( z )z 2
4
8
A equação diferença é portanto:
1
3
y[n]  y[n  1]  y[n  2]  x[n]  2 x[n  1]  x[n  2]
4
8
Exemplo 2:
H ( z )  (1  j 0,8 z 1 )(1  j 0,8 z 1 )(1  0,9 z 1 )
Y ( z)
H ( z) 
 1  0,9 z 1  0,64z 2  0,576z 3
X ( z)
y[n]  x[n]  0,9 x[n  1]  0,64x[n  2]  0,576x[n  3]
7
Causalidade e Estabilidade
Um sistema é estável se a sua resposta ao impulso é absolutamente


somável, isto é:
n
|
h
[
n
]
|


ou
|
h
[
n
]
z
| 


n  
n  
que é equivalente à condição de que a ROC inclui o círculo unitário.
Exemplo 3:
5
y[n]  y[n  1]  y[n  2]  x[n]
2
5
Y ( z )  Y ( z ) z 1  Y ( z ) z  2  X ( z )
2
 5

Y ( z ) 1  z 1  z  2   X ( z )
 2

Y ( z)
1
1
H ( z) 


X ( z ) 1  5 z 1  z  2 (1  1 z 1 )(1  2 z  2 )
2
2
ROC: 1. |z|>2; 2. 0,5<|z|<2;
3. |z|<0,5;
Causal: |z|>2
Estável: 0,5<|z|<2
8
Sistema Inverso: Hi(z)
1
G(z) = H(z)Hi(z) = 1, portanto, H i ( z ) 
H ( z)
No domínio do tempo: g[n]  h[n]  hi [n]   [n]
1
No domínio da frequência: H i (e ) 
H (e j )
Representando por uma função racional
j
M
(1  ck z )
 b0  
H ( z )    kN1
 a0 
(1  d z 1 )

1
k
k 1
1
1

0
,
5
z
Exemplo 4: H ( z ) 
1  0,9 z 1
1  0,9 z 1
H i ( z) 
1  0,5 z 1
N
 a0 
H i ( z )   
 b0 
1
(
1

d
z
 k )
k 1
M
1
(
1

c
z
 k )
k 1
Se a ROC é |z|>0,5, H(z) é causal
e estável e Hi(z) é ainda causal e
estável. Os pólos e zeros estão
dentro do círculo unitário
hi [ n ]  ( 0,5 )n u[ n ]  0,9( 0,5 )n1 u[ n  1]
9
Exemplo 4:
1  0 ,5 z 1
H( z ) 
,
1
1  0 ,9 z
z  0 ,9
1  0 ,9 z 1
Hi ( z ) 
1  0 ,5 z 1
H(z) é estável. Se a ROC de Hi(z) é |z|>0,5, então Hi(z) é causal e
estável.Observe que os pólos e zeros estão dentro do círculo unitário
hi [ n ]  ( 0,5 )n u[ n ]  0,9( 0,5 )n1 u[ n  1]
Exemplo 5:
z 1  0 ,5
H( z ) 
,
1
1  0 ,9 z
z  0 ,9
1  0 ,9 z 1  2  1,8 z 1
H i ( z )  1

z  0 ,5
1  2 z 1
Se a ROC é |z|>2, Hi(z) é causal e instável.
hi [ n ]  2( 2 )n u[ n ]  1,8( 2 )n1 u[ n  1]
Se a ROC é |z|<2, Hi(z) é estável e não causal
hi [ n ]  2( 2 )n u[ n  1]  1,8( 2 )n1 u[ n ]
10
Resposta Impulso de Funções Sistemas Racionais
• Considere a representação de expansão em frações parciais:
H z  
M N
N
Ak
1
k 1 1  d k z
 Br z  
r 0
r
onde há somente pólos de primeira ordem.
• Cada pólo (segundo termo) contribui com uma exponencial para
h[n], tal que:
M N
N
hn 
 Br  n  r   Ak d k un
n
r o
k 1
• Supondo que H(z) é causal, e que todos os pólos estão dentro do
círculo unitário.
– Se existem somente termos como os da primeira parcela, então
o sistema é chamado de FIR ( Finite Impulse Response)
– Se existem somente termos como os da segunda parcela, então
o sistema é chamado de IIR (Infinite Impulse Response) 11
Exemplo de Filtro IIR
1  2 z 1  z 2
1  2 z 1  z 2
H ( z) 

3 1 1  2
1 1
1 z  z
(1  z )(1  z 1 )
2
2
2
| z | 1
n
1
h[n]  2 [n]  9  u[n]  8u[n]
 2
Exemplo de Filtros FIR
H ( z)  1  0,9z 1  0,5z 2  0,7 z 3  0,9z 4  z 5  z 6
h[n]   [n]  0,9 [n  1]  0,5 [n  2]  0,7 [n  3]  0,9 [n  4]   [n  5]   [n  6]
a
h[n]  
0,
n
0n N
outros valores
N
H ( z )   a n z n
n 0
1  a N 1 z  N 1

1  az1
12
Resposta em Freqüência para Sistemas Racionais
• Se um sistema LTI e estável, a sua ROC inclui o circulo unitário e
conseqüentemente ele possui transformada de Fourier. Portanto a
função sistema pode ser escrita na forma.
M
H e
 
 
j
  H z 
z  e j
 
H e j  H e j exp( jARG[ H e j ]
M
H e j  
b0
a0
 1 c e
k 1
N
H e

a e
 jk
k 0
N
k 0
k
 1  c e 
M
b
 0
a0
k
k 1
N
 j
k
 1  d e 
k 1
 j
k
 j
k
 1 d e
 j
k
k 1
j 2

b e
 jk
M
 b0 
 H e H e    
 a0 
j

j
2
 (1  c e
k 1
N
k
 j
)(1  ck*e j )
 j
* j
(
1

d
e
)(
1

d

k
ke )
k 1
13
Resposta em Freqüência
M
H e 
j 2
b




 H e H e  
a
j
• Expressando H e
 
10log10 H e
j 2

j 2


 0
0
 j
* j
(
1

c
e
)(
1

c
 k
ke )
k 1
N
 j
* j
(
1

d
e
)(
1

d

k
ke )
k 1
em decibeis(dB):
unidade ganhoem dB
 
0 dB  H ( e j )  1
 20log10 H e
   20log
20 log10 H e
j

2
j
10
j
M
N
b0
 j
  20 log10 1  ck e
  20 log10 1  d k e  j
a0 K 1
k 1
• Relação entre entrada e saída
Y e j   X e j H e j 
20 log10 Y e j   20 log10 X e j   20 log10 H e j 
 b0 
H e       1  ck e j    1  d k e j 
k 1
 a0  k 1
j
M
•Zero – adição de fase
• Pólos – subtração de fase
N
14
Retardo de Grupo para um Sistema Racional


grd H ( e j )  

grd H e
j


d
ARG [ H ( e j )]
d

M
d
d
 j
  arg[1  d k e ]   arg[1  ck e j ]
k 1 d
k 1 d
N
Valor Principal Fase – Devido a periodicidade da fase, considera-se
para análise, os valores compreendidos entre  


  
ARG H e
b
 ARG 0
 a0
.

   ARG H e j   
j
e

H e j   ARG H e j   2r 




N
 M
 j
   ARG 1  ck e
  ARG 1  d k e  j  2r( w )
k 1
 k 1
15
Exemplo 1: Resposta em Frequência de filtros FIR
1, 0  n  4
h[ n ]  
fora
 0,
H( e
j
4
)  e
 jn
n 0
H ( e j )  e  j 2
1  e  j 5 e  j 5 / 2

  j / 2
 j
1 e
e
h[n]
-1
0
1
1
2
 e j5 / 2  e  j5 / 2

 e j / 2  e  j / 2

3
4
n
5




sen( 5 / 2 )
sen(  / 2 )
Resposta em frequência: a) Amplitude; b) Fase; c) Retardo de grupo
16
Exemplo 2: Resposta em Frequência de filtros FIR
1, 0  n  5
h[ n ]  
fora
 0,
H( e
j
5
)  e
 jn
n 0
H ( e j )  e  j 5 / 2
1  e  j6
e  j3

  j / 2
 j
1 e
e
h[n]
-1
0
1
1
2
 e  j3  e  j3

 e  j / 2  e  j / 2

3
4
5
6




sen( 3 )
sen(  / 2 )
Resposta em frequência: a) Amplitude; b) Fase; c) Retardo de grupo
17
n
Resposta em Freqüência de Pólo e Zero Simples
M
• Da equação que ralaciona pólos e zeros
Considerando um único pólo forma
H ( z )  1  cz 1 substituindo
H ( e j )  1  re j e  j
H( e
H( e
j
j
2
j  j 2
)  1  re e
b0
H e  
a0
c  re
j
 j
1

c
e
 k
k 1
N
 j
1

d
e
 k
k 1
j
e
1
z e
 j
 ( 1  re j e  j )( 1  re  j e j )
2
)  1  r 2  2r cos(    )
Calculando H ( e j ) em dB
| H( e j ) |dB  10log10 [ 1  r 2  2r cos(    )]
Fase: ARG | H ( e
j
rsin(    )
) | tan
1  r cos(    )
1
18
Resposta em Freqüência
de Pólo Simples
H( e
j
2
)  1  r 2  2r cos(    )
H ( e j )
em dB
10log10 [ 1  r 2  2r cos(   )]
Valor máximo:
1  r 2  2r quando     
Valor mínimo:
1  r 2  2r quando     0
19
Resposta em frequência para
um zero simples,   
r = 1; 0,9; 0,7 e 0,5.
20
Resposta em frequência para
um zero simples, real e fora
do círculo unitário.
r = 1,09; 1,25 e 2,0.
21
Sistemas Passa Tudo (All Pass)
• Um passa tudo é um sistema da forma (ou cascata destes)
z 1  a
H Ap Z  
1  az1
 
H Ap e
j 2
 j

j
e

a
1

a
*
e
 j
H Ap e j  

e
1  ae j
1  ae j
  j 1  a * e j  j 1  ae j 
 e
1
  e
 j 
j 
1  ae
1  a* e 


• Forma Geral - com pólos reais e complexos
z 1  d k M c ( z 1  ek* )( z 1  ek )
H Ap z   
1 
1
* 1
1

d
z
(
1

e
z
)(
1

e
k 1
k 1
k
k
kz )
Mr
Causal/estavel:
ek , dk  1
• Sistema passa tudo tem resposta em fase não positiva para 0<<.
• Sistema passa tudo tem sempre retardo de grupo positivo..
22
Sistema Passa Tudo
Exemplo: Passa tudo com M = N = 2Mc + Mr = 4 pólos e zeros


1
3
1
1
j

j
( z  )( z  0 ,5 )
1
4 )( z 1  0 ,8e 4 )
(
z

0
,
8
e
2
4
H Ap z  


1 1
3 1
j
j
( 1  z )( 1  z ) ( 1  0 ,8e 4 z 1 )( 1  0 ,8e 4 z 1 )
2
4
Im
Círculo
unitário
Mr  2 e Mc  1
Plano Z
pólo : re j  zero : r 1e j
0.8

4
3

3
4
Re
0.5
2
23
Sistema de Fase Mínima
• Um sistema com todos os seus pólos e zeros dentro do círculo
unitário (causal e estável) é chamado de fase mínima. E seu
inverso é ainda causal e estável.
H (e )  H ( z) z e jw
jw
2
H ( z )  H ( z )H * (
1
H( e
)
z*
H( e
j
j
2
)  H ( e j ) H * ( e j )
2
)  H ( z )H * (
1
z*
)
z e j
• Conhecendo-se H(z), sem especificar a ROC, a determinação de
h[n] não é única. No entanto, se é conhecido que o sistema é de
fase mínima, determina-se a representação única de h[n] sem a
necessidade de especificar a ROC, devido aos requisitos de seus
pólos e zeros.
24
Decomposição em um Passa Tudo e um Fase
Mínima
• Qualquer sistema racional com função sistema H(z) pode ser
escrita como:
H ( z)  Hmin ( z) H Ap ( z)
• Hmin(z) contém todos os pólos e zeros dentro do círculo unitário, em
cascata com um passa tudo HAp(z), com zeros rebatidos para fora do
círculo unitário.
• Propriedades do sistema de fase mínima Hmin(z) :
• Tem fase mínima.
• Tem retardo de grupo mínimo
• Tem energia mínima.
25
Exemplo1: Para ilustrar a decomposição considere o sistema
1  3 z 1
H( z ) 
1
1  z 1
2
1
zero : z  3; pólo : z  
2
1
1
1
1
3(  z ) 3( z  )
3
Rescrevendo H(z) H ( z )  3

1 1
1 1
1 z
1 z
2
2
Multiplicando e dividindo H(z) por ( 1  1 z 1 ) para completar o
3
passa tudo, tem-se:
1
1 1
1 1  1 1 

3( z  )( 1  z )  3( 1  z )  z  
3
3
3
3 

H( z ) 

1 1
1 1
1 1 
1 1 

( 1  z )( 1  z )  1  z
 1  z 
2
3
2
3



1
Hmin(z)
Hap(z)
26
Exemplo 2


3 j 4 1
3 j 4 1

( 1  e z )( 1  e z )

j
3
1
2
2
H( z ) 
; zeros : z   e 4 ; pólo : z 
1 1
2
3
1 z
3
Neste caso tem-se dois zeros fora do círculo unitário. Fatorando-se:




9 2  j4
2 j4
2  j4
2 j4
1
1
1
1
( e
 z )( e  z )
(z  e
)( z  e )
9
3
3
3
H( z )  4 3

1
1
4
1  z 1
1  z 1
3
3

2  j 4 1
Agora, multiplicando e dividindo H(z) por ( 1  e z )
3



 




j
j

j
j
 ( 1  2 e 4 z 1 )( 1  2 e 4 z 1 )  ( z 1  2 e 4 )( z 1  2 e 4 ) 
9


3
3
3
3
H( z )  




1 1
4

j
j
1 z

 1  2 e 4 z 1 )( 1  2 e 4 z 1 ) 
3
3
3



27
Aplicação: Compensação da Resposta em Freqüência
G (z )
s[n]
Sistema com
distorção
Sistema
compensação
H d (z )
s c [n ]
H c (z)
Hd ( z)  Hd min ( z) H Ap ( z)
H c ( z) 
1
H d min ( z )
Após a compensação:
• G(z) corresponde a um sistema passa tudo.
• O módulo da resposta em freqüência é exatamente compensada.
• A resposta em fase é modificada por um fator: H Ap (e j ). 28
Função de Transferência de um filtro
• Considere a equação diferença de um sistema linear invariante,
com coeficientes constantes:
N
N
N
N
k 1
k 1
k 1
k 1
y[n]   ak y[n  k ]   bk x[n  k ]  y[n]   ak y[n  k ]   bk x[n  k ]
Calculando a transformada Z de ambos os lados
N
N
Y ( z )  Y ( z )  ak z
k 1
k
N
 X ( z ) bk z
k
k 1
Y ( z)
 H ( z) 

X ( z)
b z
k 1
N
k
k
1   ak z  k
k 1
Reescrevendo H(z) como produto de duas funções


Y ( z) 
1
H ( z) 

N
X ( z) 
k
 1   ak z
 k 1

 N
 b z  k 
k
 
k 1



29
Representação da Equação Diferença por
Digrama de Blocos - Realização Direta I


1
y[n]   ak y[n  k ]   bk x[n  k ] H ( z )  Y ( z )  
N
k 1
k 1
X ( z) 
k
1

a
z
  k
 k 1
N
N
N
v[n]   bk x[n  k ]
k 1
N

 N
 b z  k 
k
 
k 1



y[n]   ak y[n  k ]  v[n]
k 1
 N
k 
V ( z )  H1 ( z ) X ( z )    bk z  X ( z )
 k 1





1
V ( z )
Y ( z )  H 2 ( z )V ( z )  
N

k 
 1   ak z 
 k 1

Y ( z)  H 2 ( z) H1 ( z) X ( z)
30
Diagrama de Blocos: Realização na Forma Direta II
N
w[n]   ak w[n  k ]  x[n]
k 1
N
y[n]   bk w[n  k ]
k 0


1

W ( z)  H 2 ( z) X ( z) 
N

k
 1   ak z
 k 1
Substituindo W(z)


 X ( z)



 N
k 
Y ( z )  H1 ( z )W ( z )    bk z W ( z )
 k 1



N
1


Y ( z )  H1 ( z ) H 2 ( z ) X ( z )    bk z  k 
N
 k 1
 1  a z  k
  k
 k 1


 X ( z)



31
Exemplo: Implementação de um sistema LTI
Considere o sistema LTI com função de transferência
1  2 z 1
H ( z) 
1  1,5z 1  0,9 z 2
, b0  1; b1  2; a1  1,5; a2  0,9
Implementação na forma direta I e direta II
32
Implementação usando Signal Flow Graph:
Formas Diretas
• Dada a equação diferença
N
N
N
N
k 1
k 1
k 1
k 1
y[n]   ak y[n  k ]   bk x[n  k ]  y[n]   ak y[n  k ]   bk x[n  k ]
Forma Direta I
Forma Direta II
33
Estrutura de Sistemas IIR: Forma Cascata
• Fatorando-se o numerador e o denominador de H(z), pode-se
I
escrever
H ( z)   Hi ( z)
i 1
Que pode ser disponibilizado como cascata de seções menores
H1 ( z )
H 2 ( z)

H I (z )
H (z )
• Vantagem: Seções menores.
• Desvantagem: Propagação de erro de seção para seção.
34
Realização Paralela
• Fatorando-se o numerador e o denominador de H(z), podeI
se escrever
H ( z)   Hi ( z)
i 0
Que pode ser disponibilizado como cascata de seções
menores
H1 ( z )
H1 ( z )

:
H1 ( z )
H (z )
35
Estrutura de IIR: Exemplo (Cascata)
1  2 z 1  z 2
Dado o sistema de segunda
H ( z) 
1  0.75z 1  0.125z 2
• Estrutura em cascata (não única)
 1  z 1  1  z 1 


H ( z )  
1 
1 
 1  0.5z  1  0.25z 
36
Estrutura de IIR: Exemplo (Paralela)
1
2
1

2
z

z
Dado o sistema de segunda H ( z ) 
1  0.75z 1  0.125z 2
• Parallel Structure (Not unique)
 7  8 z 1
18
25
H ( z)  8 
8

1
2
1
1  0.75z  0.125z
1  0.5z
1  0.25z 1
Forma paralela, usando
sistemas de segunda ordem
Forma paralela, usando
sistemas de primeira ordem
37
FILTROS FIR: Realização na Forma Direta
FILTROS FIR: Realização na Forma Transposta
38
FILTROS FIR: Realização na Forma Direta
Realização de um sistema FIR com fase linear com M Par
39
Realização de um sistema FIR com fase linear com M Ímpar
Simetria dos Zeros de um
sistema FIR com fase Linear
40
Projeto de Filtros Digitais
•
Dado um conjunto de especificações ou algumas restrições
com relação à:
- Resposta em amplitude
H ( e j )
- Resposta em fase H (e j )
•
.
Encontrar { am } e { bk } tal que
M
H( z ) 
 am z
m 0
K
1   bk z
k 1
M
m
k
ou
H ( e j ) 
 a m e  j m
m 0
K
1   bk e  jk
k 1
41
Projeto de Filtros Digitais
As restrições podem incluir:
• Fase zero (ou próximo) ou linear.
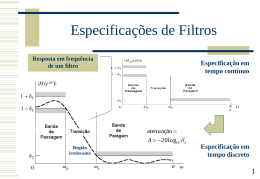
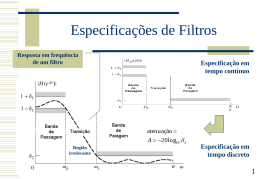
• Banda passante e frequência de corte.
• A intensidade do ripple na banda passante.
• A intensidade do ripple na banda de rejeição.
• A forma da transição entre as bandas
passante e de rejeição.
• A ordem do filtro K, M.
42
Projetos de Filtros FIR
• No caso de filtros FIR: bo=1 e b1  b2  b3      bK  0
M
Então
m
H ( z )   am z
m 0
• A resposta ao impulso unitário é:
an ; 0  n  M
h( n )  
else
 0;
• Problema: Dada as especificações sobre H ( e j ) e H (e j ) ,
encontrar {an ; n  1,...,M }
• Vantagens:
– São sempre estáveis.
– Podem ter fase linear exatas .
– Fáceis de projetar.
• Desvantagem:
– Em geral tem ordens altas, para satisfazerem as restrições.
43
Projetos de Filtros FIR
• Projetar um filtro digital FIR h(n)  H (e j ) com M+1 coeficientes
que se aproxime da resposta em frequência desejada
j
j
D( e )  D( e ) e
jD ( e j )
com
d (n) 
1
2



D ( e j )e jn d
• Geralmente d(n) não pode ser realizado por algumas razões:
– d(n) tem duração infinita D (e j ) contém descontinuidades;
– se d(n) é não causal;
– outras;
• O método da janela é o mais simples para se projetar um filtro
FIR. Consiste em se multiplicar a resposta ao impulso desejada,
por uma janela, w[n] para limitar o tamanho de h( n )  w( n )  d ( n ).
44
Projetos de Filtros FIR usando Janela
• Definindo h(n)  w(n)  d (n)
w(n)  0 for n {0,1,...,M }
• Então o filtro deve ter resposta em frequência
onde
M
H (e )   w(n)  d (n)e  jn
j
n 0
H( e
j
)  W( e
j
)* D( e
Exemplo: Janela Retangular
H( e
j
j
)
onde w( n )  W( e j ).
1; 0  n  M
w( n )  
fora
0;
M
)   d ( n )w( n )e  jn  D( e j )* W ( e j )
n 0
W (e j ) 
sin[ ( M  1) / 2]  jM / 2
e
 /2
45
46
Outras Janelas
– Hamming :
– Hanning:
0.54  0.46cos(2n / M ); 0  n  M
w(n)  
0;
else

0.5  0.5 cos(2n / M ); 0  n  M
w(n)  
0;
else

– Blackman:
0.42  0.5 cos(2n / M )  0.08cos(4n / M ); 0  n  M
w(n)  
0;
else

47
Usando o Matlab: Tipos de Janelas
w = bartlett(n)
w = bartlett(n)
w = chebwin(n,r); r:Estabelece que riple do
lóbulo lateral deve estar a r dB abaixo do
lóbulo principal.
w = hamming(n) ; n = tamanho da janela
w = hanning(n)
w = kaiser(n,beta) ; beta parâmetro que afeta a atenuação do
lóbulo lateral da transformada de Fourier. Parâmetro de um
função de Bessel modificada.
w = triang(n)
w = triang(n)
48
Projeto Filtros Digitais FIR Usando Matlab
SINTAX
h = fir1(n,Wn): defaut: Janela de Hamming;
Wn=frequência de corte de um filtro passabaixa. Para filtro passa faixa Wn=[wc1 wc2].
Exemplo: h = fir1(48,0.25);
h = fir1(48,[0.35 0.65]);
h = fir1(n,Wn,'ftype'):ftype especifica:
high para filtro passa alta com frequência de
corte Wn.
stop para filtro rejeita faixa com frequência
de corte Wn = [w1 w2]
k = fir1(48,0.25,’high’);
49
Projeto Filtros Digitais FIR Usando Matlab
h = fir1(n,Wn,window)
Window especifica a janela
h = fir1(n,Wn,'ftype',window)
Window especifica a janela
ftype especifica:
high para FPA com frequência de corte Wn.
stop para filtro rejeita faixa com frequência
de corte Wn = [w1 w2]
Exemplo:
h = fir1(34,0.48,'high',chebwin(35,30));
50
Projeto Filtros Digitais FIR
Remez : Algoritmo de Parks-McClellan projeto
de filtros FIR (otimizado).
Sintax
b = remez(n,f,a)
b = remez(n,f,a,w)
b = remez(n,f,a,'ftype')
b = remez(n,f,a,w,'ftype')
b = remez(...,{lgrid})
b = remez(n,f,'fresp',w)
b = remez(n,f,'fresp',w,'ftype')
b = remez(n,f,{'fresp',p1,p2,...},w)
b = remez(n,f,{'fresp',p1,p2,...},w,'ftype')
[b,delta] = remez(...)
[b,delta,opt] = remez(...)
51
Projeto Filtros Digitais FIR
Exemplo:
f = [0 0.3 0.4 0.6 0.7 1]; a = [0 0 1 1 0 0];
h = remez(17,f,a);
[h,w] = freqz(h,1,512);
plot(f,a,w/pi,abs(h)), xlabel ('Frequencia'),
ylabel('Amplitude') ,xlabel('Frequencia'),
ylabel('Amplitude')1.4
1.2
Amplitude
1
0.8
0.6
0.4
0.2
0
0
0.2
0.4
0.6
Frequencia
0.8
521