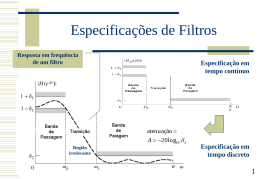
Especificações de Filtros
Resposta em frequência
de um filtro
Especificação em
tempo contínuo
atenuação 
A  20 log10  2
Região
irrelevante
Especificação em
tempo discreto
1
FIR e IIR
FIR – Finite Impulse Response Filter
(Resposta ao Impulso Finita)
M – ordem
do filtro
M
M
m 0
m 0
y[n]   bm .x[n  m]  H ( z )   bm .z  m
IIR – Infinite Impulse Response Filter
(Resposta ao Impulso Infinita)
N
M
k 0
m0
 ak . y[n  k ]   bm .x[n  m]  H ( z) 
N – ordem do filtro
M
m
b
.
z
m
m0
N
Só tem
zeros 
sempre
estáveis
Contêm
zeros e
pólos
k
a
.
z
 k
k 0
2
FIR vs IIR
 FIR



São sempre estáveis
Permitem facilmente fase linear
Podem necessitar de ordem elevada
 IIR

Menor peso computacional
3
Projecto de Filtros IIR
Conversão de Filtros Analógicos
•Aproveita os resultados dos sistemas analógicos
Transformação Bilínear
Provoca uma
transformação
na frequência
• Um mapa do plano-s para o plano-z
2
  tan( / 2)
2  1  z 1 
T

s  
T  1  z 1 
  2arctan(T / 2)
Mapa exacto seria
(AD-DSP-DA):
sT
e
z
4
Transformação Bilínear
Transforma o semi-plano complexo
esquerdo no circulo unitário!
Sistemas estáveis resultam em
sistemas estáveis
Transformação na frequência:
2  1  z 1 

s  
1 
T  1 z 
Especificações devem ser
ajustadas de forma a compensar
a transformação
1  (T / 2) s
z
1  (T / 2) s
5
Invariância ao Impulso
AK
H ( s)  
k s  sK


h(t )   AK e  sK t u[t ]
TL1
k
amostragem
AK
H ( z)  
1
1

z
z
k
k
TZ

zk  e
hn   AK zk u[n]
n
k
sk T
6
Filtros Butterworth
 São filtros que têm uma característica de
amplitude maximamente plana na banda de
passagem.
Têm a seguinte resposta em amplitude:
2
1
H c ( j) 
1  ( j / jc ) 2 N
H C ( j)  1 /( / C ) 2 N
2
A sua transformada de Laplace é
constituída apenas por pólos nas
posições:
s   e( j / 2 N )( 2k  N 1)
k
C
H ( s) 
1
N
 (1  s / s )
k
k 1
7
Filtros Chebyshev
 Permitem oscilações na banda de passagem de forma
permitir a utilização de filtros de menor ordem
relativamente ao Butterworth.
1
H c ( j) 
1   2VN2 ( / c )
2
V0 ( x)  1
V1 ( x )  x
V2 ( x)  2 x 2  1
VN 1 ( x)  2 xVN ( x)  VN 1 ( x)

H C ( j)  1 /  2 4 N 1 ( /  C ) 2 N
2

8
Filtros passa-banda
Projecto em tempo continuo
 Transformação passa-baixo passa banda
 Escolher o tal que,
B   
 Especificações
P2
P1
o2  S1 S 2
o2  P1 P 2
ou mais apertadas
TPassa  Banda (s)  TPassa  Baixo (S ) S  s 2 02
 Low  Pass
 2 0 2

B
   P 2   Low Pass  1
   P1   Low Pass  1
Bs
   S 2 / 1   Low  Pass
 
1
B Low  Pass 
2
 S 2  S 1
 
 P 2  P1
1
4
 02  B 2  2Low  Pass
9
Filtros passa-banda
o2  S1 S 2
S
P 2
P1
P1
S 2
B  P 2  P1
 S 2  S 1

 P 2  P1
Deve-se escolher P1 e P2 de forma que:
o2  P1 P 2
Mas garantindo que P1< P1real e
P2> P2real
1
S
10
Projecto de Filtros FIR
Método da Janela
Especificação de uma resposta ideal na frequência e
determinação da resposta impulsiva correspondente:
1
hd [n] 
2
H d (e j )
Multiplicação por janela:
h[n]  hd [n  d ]w[n]
Atraso da janela
1,
Janela
w[n]  
rectangular:

janela
0nM
0, cc

j
j
H
(
e
)
e
d
 d

Pode ser infinita
e não causal 
truncagem
d M /2
11
Janela Rectangular
j
W (e )  e
 jM / 2
sin[ ( M  1) / 2]
sin[ / 2]
12
Outras Janelas
Bartlett (triangular)
2n / M , 0  n  M / 2

w[n]  2  2n / M , 0  n  M / 2

0, cc

Rectangular
1, 0  n  M
w[n]  
0, cc

Hanning
0.5  0.5 cos(2 n / M ), 0  n  M
w[n]  
0, cc

Hamming
0.54  0.46cos(2 n / M ), 0  n  M
w[n]  
0, cc

Blackman
0.42  0.5 cos(2 n / M )  0.08cos(4 n / M ), 0  n  M
w[n]  
0, cc

13
Janelas
Rectangular
(o riple ou a atenuação
nunca baixam de 20dB
por maior que seja a
ordem! Fenómeno de
Gibbs)
Hamming
triangular
Blackman
Hanning
14
Janelas
15
Janela de Hanning
n'  n  M / 2
w[n]  (0.5  0.5 cos(2 n / M )) wR [n] 
w[n' ]  (0.5  0.5 cos(2 n' / M )) wR [n' ]

 
2   
2
W (e j )   ( )     
    
2 
M  2 
M

W (e j )

j
.WR (e )

WR (e j )
sin[ ( M  1) / 2]
WR (e ) 
sin[ / 2]
WR – Janela Rectangular
j
W – Janela Hanning
16
Janela Kaiser
 I 0 [  (1  [( n   ) /  ]2 )1/ 2 ]

, 0nM
w[n]  
I0 ( )
Funções de

0
,
cc

0.1102( A  8.7), A  50


  0.5842( A  21) 0.4  0.07886( A  21), 21  A  50

0.0, A  21

   s   p
Ordem
do filtro
(dB)
A8
M
2.285
A  20 log10 
Bessel
modificadas de
ordem zero
Permite trocar
largura do lobo
principal por
amplitude do
lobo secundário
  1   2
É simples obter 
e M dadas as
especificações
17
Projecto Equiriple de FIR
 Janela rectangular minimiza
1
2 
2

 H
j
d
j
2
(e )  H (e ) d

 Outro critério é o do erro máximo
max H d (e j )  H (e j )
Filtros de oscilação
constante (equiriple)
M
Resulta em filtros de menor ordem do que pelo
método das janelas
10 log( 1 2 )  13
2.324
Parks-McClellan
algorithm
18
Projecto Equiriple
 Erro quadrático mínimo (janela rectangular)

Óptimo sinais de banda larga, ex: ruído branco
 Equiriple (erro máximo mínimo)


Garante que qualquer sinal fora da banda é atenuado
pelo menos A dB
Projecto para o pior caso, ie, sinais de banda estreita
junto à banda de transição
19