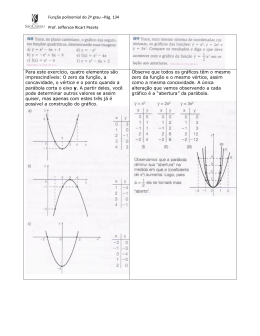
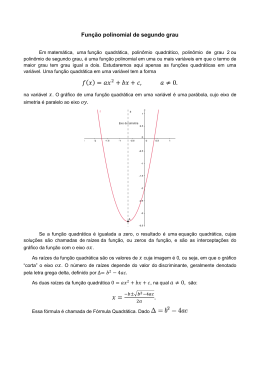
FUNÇÃO POLINOMIAL DO 2º GRAU
OU
FUNÇÃO QUADRÁTICA
Função de A em B é toda relação em que todos
os elementos de A estão relacionados a um
único elemento em B.
Quando, a função é definida por:
A função é denominada FUNÇÃO DO 1º GRAU
E a característica de sua representação gráfica é um RETA.
Chama-se FUNÇÃO POLINOMIAL DO 2º GRAU ou
FUNÇÃO QUADRÁTICA qualquer função de R em R
dada por uma lei da forma:
com a, b e c números reais e
Nomenclaturas:
Domínio 
Contradomínio
Conjunto Imagem
é o conjunto formado por todos as
ordenadas y, que representam imagens das
abscissas x, por meio da função .
(O conjunto imagem será definido no decorrer dos estudos)
A representação gráfica é dada por uma
PARÁBOLA, com concavidade voltada para
cima ou para baixo.
Para esboçar o gráfico de uma função do 1º grau, bastava
determinarmos dois pontos quaisquer, e conseguíamos
traçar o gráfico, no caso, uma reta.
No entanto, em uma função quadrática, precisamos de no
mínimo três pontos, mas é possível, muitas vezes, não
conseguirmos determinarmos a representação gráfica, pois
os pontos escolhidos podem não ser satisfatório.
Então, como proceder, de forma que sejamos
eficazes na definição da curva da função
quadrática?
Precisamos encontrar os pontos fundamentais ou notáveis:
1º) Determinar a intersecção da função com o eixo x. No caso,
calcular as RAÍZES ou ZEROS da função;
A(x’ ; 0) e B(x” ; 0)
2º) Calcular o VÉRTICE ;
3º)Determinar a intersecção da função com o eixo y .
D ( 0 ; c)
Sendo c o coeficiente da função.
Para determinar os pontos fundamentais para construir a parábola, é necessário e
obrigatório calcular:
Construir o gráfico da seguinte função g: RR, definida por:
1º) Raízes da função ( por meio da fórmula de Bháskara, ou por soma e
produto, ou ainda pelos métodos das equações incompletas, quando possível);
A(x’ ; 0) e B(x” ; 0)
2º) Calcular o vértice por meio das seguintes fórmulas:
3º) O ponto sobre o eixo y.
Como o ponto sobre o eixo y, tem abscissa igual a 0 (zero), então o valor da ordenada
sempre resultará no valor do coeficiente c , da função dada.
D ( 0 ; c)
Calculado os pontos fundamentais da parábola, basta desenhar o
plano cartesiano, localizar os pontos, e traçar a parábola
Importante:
Por meio do valor do coeficiente a na função, é possível, determinar se a
concavidade do gráfico é voltada para cima ou para baixo, antes mesmo
de representar o esboço da parábola.
Se a > 0, então a concavidade é voltada para cima ( c.v.c.).
Se a < 0, então a concavidade é voltada para baixo (c.v.b.).
O vértice é um ponto muito importante na parábola, pois por meio
deles obtemos informações significativas.
A ordenada
do vértice admite valor mínimo ou valor máximo.
Se a > 0, concavidade voltada
para cima, então a função admite
valor MÍNIMO,
.
Se a < 0, concavidade voltada
para baixo, então a função
admite valor MÁXIMO,
.
Conjunto Imagem: