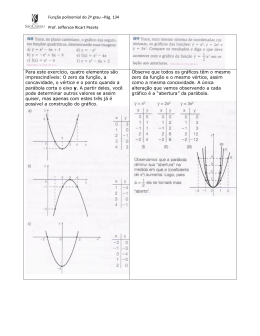
Giullia Peres da Silva
Informática-manhã
SUMÁRIO
1.
FUNÇÕES
1.1 Funções de primeiro grau
1.1.1 Exemplos de funções do primeiro grau
1.2 Funções de segundo grau
1.2.1 Exemplo de funções do segundo grau
2. AUTO AVALIAÇÃO
3. SOBRE AS AULAS
INTRODUÇÃO
Neste trabalho falarei sobre as atividades propostas pela
professora Aline de Bona. Mostrarei algumas atividades e
como fazê-las. Nesse trimestre usamos funções de primeiro e
segundo grau, sistemas lineares e em alguns momentos
representamos coisas pelos intervalos. Escolherei alguns dos
assuntos e falarei deles.
1. Funções
É função quando:
Todo domínio tem uma imagem.
Toda imagem tem um único domínio.
0
5
15
5
10
20
X
O
5
15
y=x+5
y=0+5
y=5+5
y=15+5
1.1 FUNÇÕES DO PRIMEIRO GRAU
A função do primeiro grau é representada pela
fórmula f(x)= ax+b
Esse tipo de função, quando colocada no gráfico, é
uma reta real.
1.1.1 EXEMPLOS DE FUNÇÕES DO PRIMEIRO
GRAU
Exercício:
O custo C em reais para produzir x unidades de um
componente eletrônico é dado por C(x)=18x+4500.
Qual é o custo para produzir 1000 unidades desse produto?
Resolução:
C(1000)=18.1000+4500
C(1000)=22500
1.2 FUNÇÕES DO SEGUNDO GRAU
A função para ser de segundo grau deve ser
representada pela equação f(x)= ax²+bx+c,
sendo a, b e c reais e a <> 0. Se aplicada ao
gráfico, formará uma parábola.
Na maioria das vezes, quando a equação é
completa, fazemos a báskara para descobrir os
zeros da função. Com isso, podemos saber em
que momentos a parábola corta o eixo das
abscissas.
Quando o “a” da equação é positivo, sabemos que
sua concavidade será para baixo (como se fosse um
“U”) e quando o “a” for negativo, será para cima
(como se fosse um “A”).
O que é o vértice?
O vértice é o ponto mais alto que a
função alcança quando a parábola é
negativa, e o mais baixo que ela
alcança quando é positiva.
Para descobrir em que ponto se
encontra o vértice, usamos a equação
V= -b , 2a 4a

A função, quando sua concavidade for “U”, é
decrescente até seu vértice e crescente a partir dele.
Quando for “A”, é crescente até seu vértice e
decrescente a partir dele.
Nesta parte
ela é decrescente
Nesta parte
ela é crescente
Nesta parte ela
é crescente
Nesta parte ela é
decrescente
1.2.1EXEMPLOS DE FUNÇÕES DE SEGUNDO
GRAU:
Exercício:
Uma função f do 2º grau é tal que f(0)=6,
f(1)=2, e f(-2)=20. Determine o valor de f(1/2).
Resolução:
f(x)=ax²+bx+c //Função polinomial de segundo grau
f(0)= ax²+bx+c=6
f(0)=a.0²+b.0+c-6=0
f(0)= c=6
f(1)=a.1²+b.1+6=2
f(1)=a+b+6-2=0
f(1)=a+b+4=0
f(1)= a+b=-4
f(-2)=a.(-2)²+b.(-2)+6=20
f(-2)= 4a-2b+6-20=0
f(-2)=4a-2b-14=0
f(-2)= 4a-2b=14
a+b=-4 (2)
4a-2b=14
2a+2b=-8
4a-2b=14
6a=6
a=6/6
a=1
. . . b= -5
f(x)=x²-5x+6
f(1/2)=1.(1/2)²-5.(1/2)+6
f(1/2)=0,25-2.5+6
f(1/2)= -2,25+6
f(1/2)=3,75
//Sistemas Lineares
3. AUTO AVALIAÇÃO
Eu não sei muito bem que nota me daria,
pois eu gosto muito de matemática e tenho
estudado, mas não estou tirando notas
boas. Fiz as atividades, mas só postei uma
no pbworks. Então acho que seria um 7.
Mas, ao mesmo tempo, eu sou quieta na
aula, presto bastante atenção e respeito a
professora. Então por esses aspectos,
me daria 8.
4. SOBRE AS AULAS
Eu gosto muito das aulas da professora, pois elas
são divertidas e nos acordam na segunda de manhã. A
professora é simpática e está sempre alegre, e com a corda
toda para nos receber. Eu gosto das explicações, mas, às
vezes, o conteúdo é explicado muito rápido e eu perco
alguma coisinha e acabo me perdendo toda, e depois pra
acompanhar a “sora” é meio complicado.
Também não sou muito fã do pbworks, acho meio ruim
para
matemática, e também, porque eu gosto de fazer as coisas
no papel e isso acaba me fazendo gastar o dobro do tempo
para passar os exercícios para o pb.
Acho que está tudo muito bom, só essa questão do pb que
me incomoda um pouco. Gostaria que a professora deixasse
quem quiser fazer no caderno e mostrar pra ela.