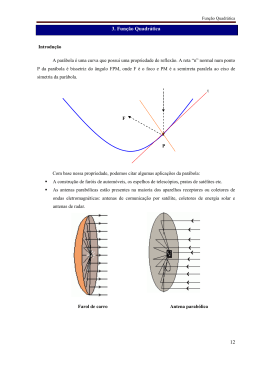
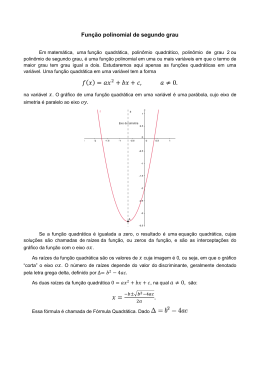
Guia do Professor
Audiovisual 07
Conteúdos Digitais
Uma parábola para Júlia
Série Mundo da Matemática
Coordenação Geral
Elizabete dos Santos
Autores
Bárbara Nivalda Palharini Alvim Souza
Karina Alessandra Pessôa da Silva
Lourdes Maria Werle de Almeida
Luciana Gastaldi Sardinha Souza
Márcia Cristina de Costa Trindade Cyrino
Rodolfo Eduardo Vertuan
Revisão Textual
Elizabeth Sanfelice
Coordenação de Produção
Eziquiel Menta
Projeto Gráfico
Juliana Gomes de Souza Dias
Diagramação e Capa
Aline Sentone
Juliana Gomes de Souza Dias
Realização
Secretaria de Estado
da Educação do Paraná
DISTRIBUIÇÃO GRATUITA
IMPRESSO NO BRASIL
2
Audiovisual “O mundo da matemática”
Episódio 7 – Uma parábola para Júlia
1 Introdução
No audiovisual “Uma parábola para Júlia”, episódio 7 do programa “O Mundo da
Matemática”, Júlia vai aprender que a perda de calorias durante uma caminhada está
relacionada com a velocidade que se imprime aos passos. Neste episódio, o aluno vai descobrir, com Rafael e Júlia, o que é uma parábola e com a função de 2º grau pode ser útil
para auxiliar na resolução de alguns problemas.
1.1 A caminhada
A caminhada é indiscutivelmente um dos exercícios aeróbicos mais adequados para os
adultos, especialmente idosos e indivíduos portadores de doenças cardíacas e metabólicas (diabetes, obesidade e excesso de triglicérides no sangue).
O ato de andar, faz parte de nossa vida e a Caminhada-Exercício é simplesmente o ato
de andar num ritmo mais acelerado elevando a frequência cardíaca, preferencialmente,
dentro da Zona Alvo de Treinamento ou Tabela de Percepção Subjetiva do Esforço. Na
década de 90, andar era a forma mais popular de exercício no mundo, superando todas
as outras formas.
Em 1957, assim que voltou da Europa, Antonio Glayr Santarnecchi fundou o Clube dos
Andarilhos de São Caetano do Sul, tornando-se o pioneiro nessa área movido pelo senso
esportivo que desenvolveu por lá.
O amor à caminhada foi aumentando no país, tanto que,no ano de 2000, em comemoração aos 500 anos do descobrimento do Brasil, foi realizada a 1ª Volta a Pé de Caçapava
com 500 km de percurso passando por locais turísticos e ecológicos da cidade.
1.2 Função Quadrática
Definição:
Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR
em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a 0.
Vejamos alguns exemplos de função quadrática:
f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
f(x) = x2 -1, onde a = 1, b = 0 e c = -1
f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
Gráfico: O gráfico de uma função polinomial do 2º grau, y = ax2 + bx + c, com a 0, é uma
curva chamada parábola.
Observação: Ao construir o gráfico de uma função quadrática y = ax2 + bx + c, notaremos sempre que:
se a > 0, a parábola tem a concavidade voltada para cima;
se a < 0, a parábola tem a concavidade voltada para baixo
3
Coordenadas do vértice da parábola
Quando a > 0, a parábola tem concavidade voltada para cima e um ponto de mínimo V;
quando a < 0, a parábola tem concavidade voltada para baixo e um ponto de máximo V.
Em qualquer caso, as coordenadas de V são .
∆ 
 b
− ,− 
 2a 4a 
Veja os gráficos:
Objetivos do episódio
•
•
•
•
•
•
O que o aluno deverá saber ao final deste episódio:
estabelecer a relação entre matemática e esportes;
encontrar uma função quadrática a partir de um conjunto de pontos;
determinar o valor máximo de uma função quadrática;
atribuir significado ao máximo de uma função quadrática;
realizar conversões entre medidas de tempo e de distância;
representar graficamente uma função quadrática.
Sugestão de atividade
Para complementar as apresentações do audiovisual, o professor pode construir com
os estudantes a função do 2º grau a que se refere a apresentação.
A partir dos dados da tabela 1 o professor orienta a representação dos dados em plano
cartesiano, conforme indica a figura 1.
MIN
60
50
45
40
30
20
10
TEMPO
HORAS
1
0.833
0.75
0.667
0.5
0.334
0.167
VELOCIDADE
Km/hora
ENERGIA CONSUMIDA (Kcal)
3
3.6
4
4.5
6
9
18
155
183.92
190.18
190.99
175.95
139.01
80.66
Tabela 1: os dados sobre a energia consumida na caminhada de 3000
4
Figura 1:
A representação gráfica dos
dados da tabela
Comentários para o professor:
É importante que o professor oriente, nesse momento, a escolha de três para construir
a função quadrática associada ao problema: E(t)= at2+bt + c com a negativo, uma vez que
a representação da figura 1 indica uma concavidade para baixo.
Para obter a função do 2º grau a partir dos três pontos escolhidos, o professor pode
trabalhar com sistema de equações, usando o método de resolução que lhe parecer mais
adequado para a turma e para as circunstâncias em que o audiovisual é usado.
4 Avaliação
A avaliação pode ser realizada durante todo o desenvolvimento das atividades, por
meio de questionamentos. O professor pode aproveitar as respostas dos alunos para fazer as intervenções que julgar necessárias.
O professor pode pedir que os alunos, divididos em grupos escolham diferentes conjuntos de três pontos e, ao final, façam comparações entre os resultados obtidos.
É muito importante que o professor mantenha os alunos ligados ao foco da atividade
(ver a velocidade ideal que se deve imprimir à caminhada para otimizar o consumo de
calorias) os oriente na apresentação da resposta. Caso contrário, eles podem, ao se envolverem com os cálculos, perder o foco do problema.
5
Condigital
Realização: