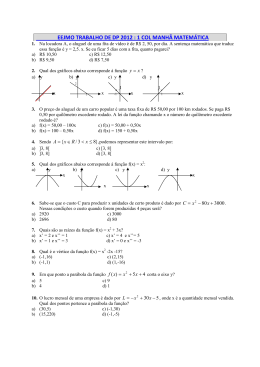
CENTRO UNIVERSITÁRIO DE VOLTA REDONDA
CENTRO INTEGRADO DE TECNOLOGIA
PROGRAMA DE APOIO À APRENDIZAGEM PARA OS CURSOS DE
ENGENHARIA
LISTA DE EXERCÍCIOS – Nº 06
Disciplina: MATEMÁTICA
Data: 27/10/2012.
1ª Questão:
Dada a função f(x)= 1-5x,calcule:
a)f(0)=
b)f(-1)=
2ªQuestão:
O custo de um produto de uma indústria é dado por C(x)=250 + 10x,sendo x o número de
unidade produzidas e C(x) o custo em reais. Qual é o custo de 1000unidades desse produto?
3ª Questão:
Determine os zeros das seguintes funções:
a)y= x²+2x
b)y=x²-7x+10
c)y=4-x²
4ª Questão:
Calcule os zeros das seguintes funções do 1ºgrau:
a)y= x+3
c)y= 4x-16
b)y= -2x+4
5ª Questão:
Determine o valor de
√
para f(x) = x -
√
.
6ª Questão:
Determine o valor de a para que se tenha f(3) = 8 na função f(x) = ax + ½.
7ª Questão:
Calcular as coordenadas do vértice da parábola correspondente a g (x) = - x² - 5x - 7
8ªQuestão:
A concavidade da parábola dada por y = (- m + 1)x² + nx + p está voltada para cima se, e
somente se:
a) m > 1;
c) n > 0:
b) m < 1;
d) p > 0.
CENTRO UNIVERSITÁRIO DE VOLTA REDONDA
CENTRO INTEGRADO DE TECNOLOGIA
PROGRAMA DE APOIO À APRENDIZAGEM PARA OS CURSOS DE
ENGENHARIA
9ª Questão:
Encontre a lei de formação e identifique o esboço gráfico que representa a situação abaixo.
Antônio Carlos pegou um táxi para ir à casa de sua namorada. O valor cobrado (y)
engloba o preço da parcela fixa (bandeirada) de R$4,00 mais R$1,60 por quilômetro
rodado.
GRÁFICOS:
10ª Questão:
Um vendedor recebe um salário fixo e mais uma parte variável, correspondente à comissão
sobre o total vendido em um mês. O gráfico seguinte informa algumas possibilidades de
salário em função das vendas.
Determine o valor das vendas mensais sabendo que o salário foi de R$ 900,00.
CENTRO UNIVERSITÁRIO DE VOLTA REDONDA
CENTRO INTEGRADO DE TECNOLOGIA
PROGRAMA DE APOIO À APRENDIZAGEM PARA OS CURSOS DE
ENGENHARIA
11ª Questão:
Em relação à função f(x) = -3x2 + 2x + 8, responda:
a) Quais são os zeros de f?
b) A parábola que representa a
função tem concavidade voltada
para cima os para baixo?
c) A função possui valor mínimo ou
valor máximo?
d) Quais as coordenadas do vértice
da parábola que representa a
função?
e) Quais as coordenadas dos pontos
em que a parábola corta o eixo x?
f) Quais as coordenadas do ponto em
que a parábola corta o eixo y?
g) Qual é a imagem de f?
12ª Questão:
Considerando o lançamento de um dardo cuja trajetória pode ser descrita pela parábola que
representa a função
, sendo x uma medida em metros.
a) Qual a distância d obtida nesse
lançamento?
b) Qual a altura máxima h atingida
pelo dardo?
13ª Questão:
Seja a função :
, √ ,
a) Calcular
,
b) Determinar os elementos de
√
cuja imagem pela vale 2.
14ªQuestão:
A soma do coeficiente angular com o coeficiente linear da reta representada no gráfico
acima é:
a) -3
d) 4
b) 0
e) 9
c) 3
CENTRO UNIVERSITÁRIO DE VOLTA REDONDA
CENTRO INTEGRADO DE TECNOLOGIA
PROGRAMA DE APOIO À APRENDIZAGEM PARA OS CURSOS DE
ENGENHARIA
15ª Questão:
Determine m, de modo que a parábola definida pela função:
a)
b)
tenha concavidade voltada para baixo
tenha concavidade voltada para cima.
16ª Questão:
O número de pontos de interseção da parábola
é:
a) 0
b) 1
c) 2
com a reta
d) 3
e) 4
17ª Questão:
(UFPE) O custo C, em reais, para se produzir n unidades de determinado produto é dado
por C 2 510 100n n' . Quantas unidades deverão ser produzidas para se obter o
custo mínimo?
18ª Questão:
Uma indústria implantou um programa de prevenção de acidentes de trabalho. Esse
programa prevê que o número ( de acidentes varie em função do tempo ) (em anos) de
acordo com a lei (
,
, ). Nessas condições, quantos anos essa indústria levará
para erradicar os acidentes de trabalho?
19ª Questão:
(Vunesp-SP) Adaptado. Uma pessoa pesando num certo momento 156 kg, recolhe-se a um
spa onde anunciam perdas de peso de até 2,5 kg por semana. Suponhamos que isso
realmente ocorra. Nessas condições:
a) Encontre uma fórmula que expresse o peso mínimo P que essa pessoa poderá atingir
após n semanas.
b) Calcule o número de semanas completas que a pessoa deverá permanecer no spa para
sair de lá com 81kg de peso.
20ªQuestão:
Suponha que um grilo, ao saltar do solo, tenha sua posição no espaço descrita em função do
tempo (em segundos) pela expressão * )
)
) , onde * a altura atingida em metros.
a) Em que instante t o grilo retorna ao solo?
b) Qual a altura máxima em metros atingida pelo grilo?
CENTRO UNIVERSITÁRIO DE VOLTA REDONDA
CENTRO INTEGRADO DE TECNOLOGIA
PROGRAMA DE APOIO À APRENDIZAGEM PARA OS CURSOS DE
ENGENHARIA
GABARITO:
1ª Questão:
a)1
b)6
, -. ,
2ªQuestão:
R$ 10.250,00
f) (0 , 8)
0
, 0 e ( 2, 0)
1 ( 2
3ª Questão:
a)0 e -2
b)2 e 5
c)-2 e 2
12ª Questão:
a) 88 m
b) 22 m
4ª Questão:
a)-3
b)2
c)4
13ª Questão:
a)
,
,
b)
,
5ª Questão:
- √2
14ªQuestão:
e)
6ª Questão:
5/2
15ª Questão:
a)
4
7ª Questão:
,
8ªQuestão:
b
9ª Questão:
y = 1,60 x + 4 / Gráfico: (a)
10ª Questão:
O valor das vendas será de R$12000,00
11ª Questão:
+
e 2
b) voltada para baixo.
c) valor máximo.
/
b)
√ 03
5
16ª Questão:
c)
17ª Questão:
50 unidades
18ª Questão:
)
+678
19ª Questão:
a) 9
, 6
b) 6
80 +6+8
20ªQuestão:
a) )
8
b) )
,:
7; : <
√
Nome do arquivo: LISTA 6 - 2 semestre
Diretório:
D:\Docs\Windows XP
Modelo:
C:\Documents and Settings\Windows XP\Dados de
aplicativos\Microsoft\Modelos\Normal.dotm
Título:
PROVA P1 de CÁLCULO I
Assunto:
Autor:
Usuario
Palavras-chave:
Comentários:
Data de criação:
26/10/2012 20:45:00
Número de alterações:
2
Última gravação:
26/10/2012 20:45:00
Salvo por:
Windows XP
Tempo total de edição:
0 Minutos
Última impressão: 26/10/2012 20:47:00
Como a última impressão
Número de páginas:
5
Número de palavras: 780 (aprox.)
Número de caracteres: 4.212 (aprox.)