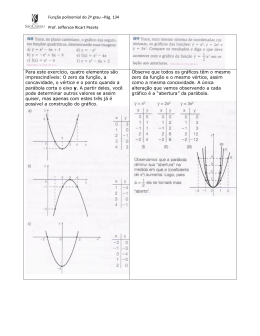
( UFSC ) Seja f(x) = ax + b uma função linear. Sabe-se que f(-1) = 4 e f(2) = 7. Dê o valor de f(8). y = ax + b f(-1) = 4 (-1, 4) 4 = a(-1) + b f(2) = 7 (2, 7) 7 = a(2) + b - a b 4 2a b 7 a=1 f(x) = ax + b f(x) = 1.x + 5 f(x) = x + 5 Logo: f(8) = 8 + 5 f(8) = 13 b=5 A semi-reta representada no gráfico seguinte expressa o custo de produção C, em reais, de n quilos de certo produto. C(reais) Se o fabricante vender esse produto a R$ 102,00 o quilo, a sua porcentagem de lucro em cada venda será? 180 80 0 20 Função do 1º grau: f(x) = a.x+ b P1(0,80) P2(20,180) x(quilogramas) 80 = a.0 + b b = 80 f(1) = 5.1+ 80 f(1) = 85 R$ 85 100% 20a = 100 R$102 a=5 x = 120% 180 = a. 20 + 80 f(x) = a.x+ b f(x) = 5.x+ 80 LUCRO DE 20% x Em relação a função f(x) = x2 – 6x + 8 definida de , determine: a) sua intersecção com o eixo y b) sua intersecção com o eixo x c) seu vértice d) Imagem da função e) A área do triângulo cujos vértices são o vértice da parábola e seus zeros As dimensões de um retângulo são dadas em centímetros, pelas expressões: 2x e (10 – 2x) com 0 < x < 5. Determinar, neste caso, o valor máximo da área em cm2 , que esse retângulo pode assumir. Área 10 – 2x yV Vértice 2x A = base x altura A = 2x . (10 – 2x) 0 A(x) = – 4x2 + 20x a=-4 b = 20 5/2 5 c=0 RAÍZES OU ZEROS DA FUNÇÃO 0 = – 4x2 + 20x x2 - 5x = 0 x1 = 0 x2 = 5 Área Máxima é o yv A(5/2) = – 4(5/2)2 + 20(5/2) A(5/2) = 25cm2 EXERCÍCIOS EXTRAS 03) GABARITO: C EXERCÍCIOS EXTRAS 01) GABARITO: A FUNÇÃO COMPOSTA Sejam f(x) = 2x + 3, g(x) = x – 5 e h(x) = 3x – 1. Calcule f(g(h(3)) f(x) = 2x + 3 f(3) = 2.3 + 3 f(3) = 6 + 3 f(3) = 9 g(x) = x – 5 g(8) = 8 – 5 g(8) = 3 h(x) = 3x – 1 h(3) = 3.3 – 1 h(3) = 9 – 1 h(3) = 8 FUNÇÃO INVERSA Encontre a inversa da função f(x) 2x - 1 x 3 f(x) 2x - 1 x 3 x= 2 y 1 y 3 x(y – 3) = 2y – 1 xy – 3x = 2y – 1 xy – 2y = 3x – 1 xy – 2y = 3x – 1 y(x – 2) = 3x – 1 y= 3x 1 x2 f (x) 1 3x 1 x 2
Baixar