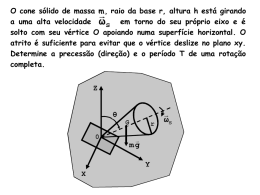
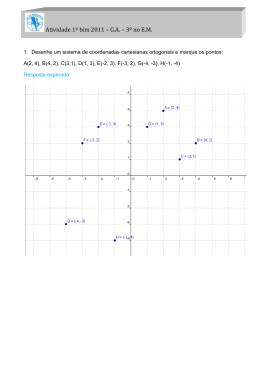
MATEMÁTICA E SUAS TECNOLOGIAS
Professor Robério Bacelar
Resolução
1. Resposta correta: A
2. Solução 1: Como os eventos são independentes, podemos fazer:
Solução 2: O número de possibilidades de retirada de 2 garrafas de
suco quaisquer pode ser calculado como:
Para duas garrafas de suco de sabores iguais, temos:
.
Como o composto é o 1,4-dibromobutano, só poderemos substituir os
hidrogênios nos carbonos “das pontas”, ou seja,
3 . 3 = 9 maneiras.
A probabilidade pode ser calculada, então
.
Resposta correta: A
5. Por definição, uma aliança será de 18 quilates se
.
Assim, a variância das notas finais é
.
Resposta correta: E
A área da parte removida é equivalente à área de um quadrado de
lado x somada com a área de um trapézio isósceles de base maior 14,
base menor x e altura 12 – x, ou seja,
Portanto, a área será mínima para
Resposta correta: D
9. Área da secção transversal do cilindro: A1 = p ⋅ 12 = p cm2. Área da
maior fatia: A2 = π ⋅ 32 – π ⋅ 12 = 8π cm2. Logo, a área da maior fatia será
8 vezes a área da secção transversal do cilindro.
Resposta correta: E
10.Basta pensar em todas as permutações das seis atividades,
desconsiderando a troca entre as atividades de sacar o dinheiro e
pagar as contas. Assim, temos
Resposta correta: E
11. Considere a figura a seguir.
de sua massa for
de ouro, sendo 1 ≤ n ≤ 18, com n ∈ N. Então, inicialmente a aliança era
de 15 quilates:
= 1,077,
8. Considere a figura a seguir.
4. Como o círculo está dividido em 6 arcos de 60°, os pontos A, B, C, D,
E e F são vértices de um hexágono regular.
O diâmetro é de 400 metros, logo o raio do círculo é de 200 m. O que
nos dá
AB = AF = 200 m.
Ligando os pontos C e D, temos o triângulo ACD, que é retângulo em
C. Usando o Teorema de Pitágoras:
AD2 = AC2 + CD2
4002 = AC2 + 2002 ⇒ AC2 = 2002 ⋅ 3
AC =
O percurso total tem comprimento:
2AB + 2AC + 2AD + 2AE + 2AF =
= 2(200 +
+ 400 +
+ 200)
= 2(800 + 400 )
= 1 600 + 800 ⋅ 1,7
≅ 2 960 m
Resposta correta: B
seja, o aumento no poder de compra passou a ser de
o que dá um aumento de 0,077 = 7,7%.
Resposta correta: B
Resposta correta: C
12 + 3x = 10 + 4x
x = 2 g.
Resposta correta: C
7. A média das notas finais é
Assim, a probabilidade de escolher garrafas de mesmo sabor será:
3. Apesar de esta questão se encaixar mais em um contexto de
Química do que de Matemática, damos aqui uma explicação acerca
da probabilidade envolvida. O primeiro passo é descobrir como é o
butano para que saibamos exatamente quantas são as maneiras de
substituirmos dois bromos. Então,
|
|
|
|
—C—C—C—C—
|
|
|
|
Temos 10 hidrogênios para retirarmos, ou seja, queremos dois entre 10:
.
em que x é a massa do ouro puro adicionada. Calculando x:
6. Suponha que o salário seja de R$ 100,00. Após dois anos, como o
aumento é de 10% ao ano, o novo salário será R$ 121,00. Agora,
digamos que com o salário de R$ 100,00 a pessoa possa comprar
R$ 100,00 (claro). Como a inflação é de 6% ao ano, após dois anos,
a despesa de R$ 100,00 passa para o valor de R$ 112,36. Portanto,
hoje, com o salário de R$ 121,00, pode-se comprar R$ 112,36, ou
,
em que m é a massa de ouro inicial. Calculando m:
m = 2,5 g.
Para que a aliança seja de 18 quilates:
,
1
= 6 ⋅ 5 ⋅ 4 ⋅ 3 = 360 possibilidades.
MATEMÁTICA E SUAS TECNOLOGIAS
O primeiro trajeto da formiga é do vértice G para o vértice C, em
seguida, do vértice C para o vértice D e, finalmente, do vértice D para
o vértice E, pois DE é uma reta reversa a CG.
Resposta correta: E
ANOTAÇÕES
12. Resposta correta: C
13. Resposta correta: D
14.A base pode ser pintada com 6 cores e as faces laterais de
PC5 = 4! = 24 formas. Portanto, o total de formas de pintarmos a
pirâmide é 6 ⋅ 24 = 144.
Resposta correta: B
15. Quantidade de chuva em mm: 100 + 100 + 300 + 100 + 50 + 50 = 700
mm. Área da base do telhado: 8 . 10 = 80 m2. 700 mm de chuva
correspondem a 700 litros por m2. Logo, o telhado captou 80.700 =
56 000 litros (56 m3) de água.
4 ⋅ 2 ⋅ h = 56 ⋅ 1,1
h = 7 ⋅ 1,1 = 7,7 m.
Resposta correta: E
CRCA/Rev.:CAR/EDG
2