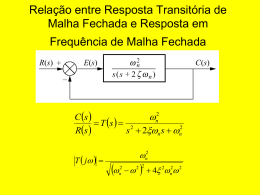
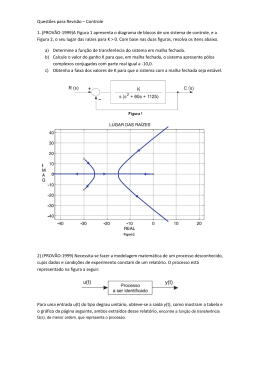
Critério de Nyquist
• Se um contorno que envolve toda o semi-plano
direito for mapeado através de G(s)H(s), então o
número de pólos a malha fechada Z, no semiplano direito é igual ao número de pólos de
malha aberta P, que estão no semi-plano direito
menos o número de rotações no sentido antihorário N, em torno do ponto -1, isto é, Z=P-N.
O mapeamento gerado é conhecido como
diagrama de Nyquist, ou gráfico de Nyquist de
G(s)H(s);
• N é positivo quando esta no sentido anti-horário
em torno do ponto -1
Exemplos de mapeamento:
a. o contorno não envolve os pólos a malha fechada;
b. o contorno envolve os pólos a malha fechada
Exemplo
14  30 j43   
G jw  500
14  30  43   
2
2
3
2
3 2
Demonstrando a
estabilidade de Nyquist:

120  71     j 154  14 
G j  
8     36
2
4
2 2
3
2
Exemplo: Determine a faixa de ganho para estabilidade, e
a frequência de oscilação na estabilidade marginal
K
Gs  
ss  3s  5
G j  


  15   
 8 2  j 15   3
64 4
2
2 2
a. Contorno e lugar das raízes do sistema que é estável
para valor pequeno de ganho e instável para valor grande
de ganho;
b. diagrama de Nyquist
a. Contorno e lugar das raízes do sistema que é instável
para valores pequenos de ganho e estável para valores
grandes de ganho;
b. diagrama de Nyquist
a. Porção do contorno a ser mapeada para o Exemplo;
b. diagrama de Nyquist do mapeamento do eixo
imaginário positivo

4  4   j   6 
G j  
4  4     6 
2
2 2
3
3
2
Diagrama de Nyquist mostrando as margens de ganho e de fase
• Margem de ganho, GM : é a mudança de
ganho de malha aberta, expresso em
decibéis (dB), necessária para no ponto
com fase 180º, tornar o sistema de malha
fechada instável;
• Margem de fase, ΦM: é mudança no valor
da fase de malha aberta no ponto de
ganho unitário, expresso em graus,
necessário para tornar o sistema de malha
fechada instável;
Exemplo: Utilize o Diagrama de Bode para determinar a faixa de
valores de K para que o sistema mostrado abaixo seja estável.
Gs  
K
s  2s  4s  5
Margens de ganho e de fase nos diagramas de Bode