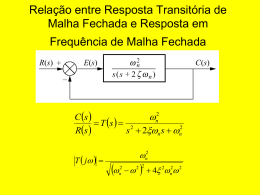
Questões para Revisão – Controle
1. (PROVÃO-1999)A Figura 1 apresenta o diagrama de blocos de um sistema de controle, e a
Figura 2, o seu lugar das raízes para K > 0. Com base nas duas figuras, resolva os itens abaixo.
a) Determine a função de transferência do sistema em malha fechada.
b) Calcule o valor do ganho K para que, em malha fechada, o sistema apresente pólos
complexos conjugados com parte real igual a -10,0.
c) Obtenha a faixa dos valores de K para que o sistema com a malha fechada seja estável.
2) (PROVÃO-1999) Necessita-se fazer a modelagem matemática de um processo desconhecido,
cujos dados e condições de experimento constam de um relatório. O processo está
representado na figura a seguir:
Para uma entrada u(t) do tipo degrau unitário, obteve-se a saída y(t), como mostram a tabela e
o gráfico da página seguinte, ambos extraídos desse relatório, encontre a função de transferência
G(s), de menor ordem, que representa o processo.
3. (ENADE-2005) Considere o sistema linear representado pelo seguinte diagrama em blocos:
onde u1(t) e u2(t) representam duas entradas, y(t), a saída do sistema e S1 e S2 são assim
modelados:
• função de transferência de S1:
• equação diferencial que representa S2:
Determine:
a) a função de transferência
b) a saída y(t) para u1(t) = D(t) e u2(t) = 0, onde D(t) representa a função degrau unitário
(Considere as condições iniciais nulas.)
c) a saída y(t) para u1(t) = D(t) e u2(t) = D(t) − D(t−2) (Considere as condições iniciais nulas.)
4. (ENADE-2008) A Função de Transferência de um levitador eletromagnético pode ser
aproximada por:
sendo Y(s) a Transformada de Laplace da saída do sistema (a posição do objeto levitado) e U(s)
a Transformada de Laplace da entrada (no caso, a corrente de um eletroímã). Para uma
entrada em degrau unitário, qual é o valor da saída quando o tempo tende para infinito?
(A) – 2
(B) zero
(C) + 1
(D) + 2
(E) infinito
5. (ENADE-2008) Alguns tipos de balança utilizam,
em seu funcionamento, a relação entre o peso ܲ e
a deformação elástica ߜ que ele provoca em uma
mola de constante elástica ‫ܭ‬, ou seja, ܲ = ‫ߜ ݔ ܭ‬
(Lei de Hooke). Ao se colocar certa mercadoria no
prato de uma balança desse tipo, a deformação ߜ
não ocorre instantaneamente. Existe um
movimento transiente que depende de outro
parâmetro: o nível de amortecimento no
mecanismo da balança, dado pelo parâmetro
adimensional
ߞ
denominado
fator
de
amortecimento.
O movimento transiente, a partir do instante em
que a mercadoria é colocada no prato da balança,
pode ser descrito por 3 equações diferentes (e tem
comportamentos diferentes), conforme o valor de
ߞ.
Com base nessas informações, conclui-se que a
balança indica o valor da massa mais rapidamente
quando:
(A) ߞ < 0.
(B) ߞ = 0.
(C) 0 < ߞ < 1.
(D) ߞ = 1.
(E) ߞ > 1.
6. (ENADE-2008) Um engenheiro recebeu como tarefa projetar um sistema de controle de
temperatura para forno elétrico. No entanto movido por uma restrição de componentes ele se
viu obrigado a utilizar um elemento somador em vez de um elemento subtrator, normalmente
empregado
ado no cálculo de erro de controle. Dessa forma ele chegou ao seguinte diagrama de
blocos para realizar o projeto de controle empregando uma ação Proporcional-Integral
Proporcional
(PI):
Nesse diagrama, Tref(s) corresponde a referência de temperatura e T(s), a temperatura
temper
da
planta (forno elétrico). Nessa situação, considere as afirmações a seguir.
1. O sistema será instável se forem escolhidos kp<1 e ki<0.
2. A letra a esta correta porque um sistema dinâmico linear, com malha de realimentação
utilizando um elemento somador,
somador será sempre instável.
Analisando as afirmações acima, conclui-se
conclui que:
(A)
(B)
(C)
(D)
(E)
As duas afirmações são verdadeiras e a segunda justifica a primeira.
As duas afirmações são verdadeiras e a segunda não justifica a primeira.
A primeira afirmação é verdadeira e a segunda
segu
é falsa.
A primeira afirmação é falsa e a segunda é verdadeira.
As duas afirmações são falsas.
7. (Concurso Petrobras-2006)
2006) Sabe-se
se que um motor de corrente contínua pode ser
representado por uma função de transferência de primeira ordem quando se relaciona
rel
a
velocidade W(s) de rotação de seu eixo com a tensão V(s) aplicada aos terminais de
alimentação. A figura abaixo apresenta o Diagrama de blocos do sistema de Controle de
velocidade do motor.
Nesse sistema de malha fechada, o erro estacionário:
(A)
(B)
(C)
(D)
(E)
Será eliminado com a adição de um controlador integrador.
Será eliminado com a adição de um controlador derivativo.
Será eliminado com a adição do controlador que foi implementado.
Aumentará quando o ganho KP aumentar
Aumentará quando for adicionado um controlador integrador.
8. (Concurso Petrobras 2008) Uma determinada planta industrial apresenta o comportamento
dinâmico semelhante ao de um modelo linear de segunda ordem, quando submetida à
aplicação de um degrau em sua entrada. Observa-se na saída da planta que a resposta possui
uma ultrapassagem máxima de 25% e algumas poucas oscilações amortecidas até alcançar o
valor de regime permanente. Neste caso, o comportamento da planta é:
(A) superamortecido, e os pólos do modelo estão localizados sobre o semi-eixo real
negativo.
(B) criticamente amortecido, e os pólos do modelo estão localizados no semiplano s
direito.
(C) subamortecido, e os pólos do modelo estão localizados sobre o semi-eixo real
negativo.
(D) subamortecido, e os pólos do modelo são complexos conjugados e estão localizados
no semiplano s esquerdo.
(E) subamortecido, e os pólos do modelo estão localizados sobre o eixo imaginário,
simetricamente posicionados em relação à origem.
9. (Concurso da Petrobras 2008)
A figura acima apresenta o diagrama do lugar das raízes, para o ganho ‫ > ܭ‬0, de uma planta
de terceira ordem, realimentada por um compensador de primeira ordem. Considerando ߣ1 ,
ߣ2 valores reais positivos tais que ߣ1 > ߣ2 > 0, é correto afirmar, a partir do diagrama, que a
planta em malha:
(A)
(B)
(C)
(D)
(E)
aberta é estável.
fechada somente é estável na faixa de ganho 0 ≤ ‫ߣ ≤ ܭ‬ଵ .
fechada somente é estável na faixa de ganho ‫ߣ ≥ ܭ‬ଵ .
fechada somente é estável na faixa de ganho ߣଶ ≤ ‫ߣ ≤ ܭ‬ଵ .
fechada é estável para todo valor de ganho ‫ ≥ ܭ‬0.
10. (Concurso da Petrobras 2008)
Um Disk-driver magnético requer um motor para posicionar a cabeça de leitura do disco, cujo
ଵ଴ఛ
sistema é modelado pela função ‫ܩ‬ሺ‫ݏ‬ሻ = ௦ሺఛ௦ାଵሻ onde ߬ = 0,25 segundo. Considerando um
compensador do tipo ‫ܪ‬ሺ‫ݏ‬ሻ =
௄
௦ା଼
e usando a estrutura de realimentação mostrada na figura
acima, qual o valor do ganho K no limiar para a instabilidade?
(A) 5,6
(B) 8,2
(C) 38,4
(D) 384,0
(E) 820,0
11. (Concurso da Casa da Moeda –Eng. Eletricista -2009)
A figura acima apresenta o esboço de um diagrama do lugar das raízes (root locus) de um
sistema de controle com realimentação de saída, por meio de ganho proporcional variando
positivamente. Analisando o diagrama apresentado, é correto afirmar que
(A)
(B)
(C)
(D)
(E)
o sistema em malha fechada é sempre instável.
o sistema é sempre estável, quando os pólos de malha fechada são reais e iguais.
a função de transferência de malha aberta é instável.
a função de transferência de malha aberta possui um pólo e dois zeros.
a função de transferência de malha aberta do sistema é de terceira ordem.
12. (Concurso da Casa da Moeda –Eng. Eletricista -2009)
O diagrama em blocos da figura acima mostra um sistema linear controlado por uma
realimentação de saída do tipo proporcional. O intervalo de variação do ganho K para que o
sistema permaneça estável é
(A)
(B)
(C)
(D)
(E)
0≤K≤2
0≤K≤5
0≤K≤8
2<K<∞
0,5 < K < ∞
13. (Concurso da Casa da Moeda – Eng. Eletronico – 2005) Com relação ao gráfico do “Lugar
das Raízes”, pode-se dizer que:
(A) consiste em um traçado no plano complexo s que representa a posição dos pólos de
malha fechada de uma planta, à medida que é variado o ganho.
(B) consiste em um traçado do diagrama polar da função de transferência de malha
aberta GH(s) e permite tirar conclusões sobre a estabilidade em malha fechada do
sistema.
(C) consiste em um diagrama de resposta em freqüência do sistema em malha aberta.
(D) os traçados iniciam-se nas posições dos zeros de malha aberta e se finalizam nas
posições dos pólos de malha aberta.
(E) os traçados iniciam-se nas posições dos zeros de malha aberta e se finalizam na
origem do gráfico, à medida que o ganho aumenta.
14. (Concurso da Casa da Moeda – Eng. Eletronico – 2005) O diagrama da figura abaixo mostra
uma malha de realimentação, característica de sistemas de controle. Para que a função de
transferência do sistema em malha fechada garanta a existência de dois pólos imaginários
puros, o valor do ganho K deverá ser:
(A) 50
(B) 300
(C) 500
(D) 750
(E) 1200
15.(Departamento de Controle de Espaço Aéreo – Eng Eletrônico – 2009)
A figura acima mostra o diagrama em blocos de um sistema em malha fechada, cujo modelo
௄
da planta é ‫ܩ‬ሺ‫ݏ‬ሻ = ௦య ା଻௦మ ାଵ଴௦ . Qual o valor de K que torna este sistema em malha fechada
puramente oscilante?
(A) 120
(B) 70
(C) 54
(D) 35
(E) 18
16. (Concurso da Petroquímica Suape – Eng. De Processamento – 2009) Seja o diagrama de
blocos em malha fechada, no qual um processo de 2a ordem é controlado por um controlador
P, exibido na figura abaixo.
Para um degrau unitário no set-point SP(s) = 1/s e supondo Kc = 4, o offset entre o set-point
SP(t) e a variável controlada PV(t) será
(A) – 0,8
(B) nulo
(C) 0,2
(D) 0,8
(E) 1
17. (Concurso da Transpetro – Eng. Automação – 2008) Um determinado sistema físico pode
ser modelado através da seguinte equação diferencial ordinária:
onde u(t) e y(t) representam, respectivamente, os sinais de entrada e de saída do sistema. A
função de transferência ‫ܩ‬ሺ‫ݏ‬ሻ = ܻሺ‫ݏ‬ሻ/ܷሺ‫ݏ‬ሻ deste sistema é:
18. (Concurso da SANEPAR-2006) Com relação ao controlador PID, considere as seguintes
afirmativas:
1. O termo P refere-se ao Controlador Proporcional, que irá reduzir o tempo de subida e
eliminar o erro em regime estacionário.
2. O termo I refere-se ao Controlador Integral, que irá aumentar a estabilidade do sistema
e eliminar o erro em regime estacionário.
3. O termo D refere-se ao Controlador Derivativo, que irá melhorar a resposta transitória,
sem influir no erro em regime estacionário.
4. O termo P refere-se ao Controlador Proporcional, que irá melhorar a estabilidade do
sistema, mas não eliminará o erro em regime estacionário.
5. O termo D refere-se ao Controlador Derivativo, que irá tornar o sistema mais lento.
Assinale a alternativa correta:
a)
b)
c)
d)
e)
Somente as alternativas 1, 2 e 5 são verdadeiras.
Somente as alternativas 1 e 4 são verdadeiras.
Somente as alternativas 2 e 4 são verdadeiras.
Somente as alternativas 2, 3 e 5 são verdadeiras.
Somente as alternativas 3 e 4 são verdadeiras.
19. Considere o esquema representado a seguir:
As funções de Transferência ܻሺ‫ݏ‬ሻ/ܴሺ‫ݏ‬ሻ e ܻሺ‫ݏ‬ሻ/ܹሺ‫ݏ‬ሻ são dadas por:
20. (Concurso da SANEPAR-2006) A finalidade do projeto de engenharia de controle é obter a
configuração, as especificações e a identificação dos parâmetros-chave de um sistema
proposto para atender a uma necessidade real. A cerca disso, considere as seguintes
afirmativas:
1. Pode-se admitir a linearidade de muitos elementos mecânicos e elétricos sobre um
domínio razoavelmente amplo de valores das variáveis. Esse não é usualmente o caso
de elementos térmicos e fluidos, que são mais freqüentemente não-lineares em sua
essência.
2. Um sistema linear não satisfaz as propriedades de superposição e homogeneidade.
3. Por constituir uma descrição do tipo entrada-saída do comportamento do sistema, a
função de transferência não é utilizada para representar a relação que descreve a
dinâmica do sistema sob consideração.
4. O método da transformada de Laplace substitui a solução mais difícil de equações
diferenciais pela solução mais fácil de equações algébricas.
Assinale a alternativa correta.
a)
b)
c)
d)
e)
Somente as afirmativas 1, 2 e 3 são verdadeiras.
Somente as afirmativas 1 e 4 são verdadeiras.
Somente as afirmativas 2 e 4 são verdadeiras.
Somente as afirmativas 1, 2 e 4 são verdadeiras.
Somente as afirmativas 3 e 4 são verdadeiras.
21. (Concurso para Engenheiro da Marinha) Pretende-se projetar um controlador para o
sistema G(s)=1/[s(Js+b)] como ilustrado na figura abaixo. Onde r(t) é o sinal de referência, e(t)
é o erro do sistema, y(t) é a variável controlada, d(t) é o sinal de distúrbio, e H(s) a função de
transferência do controlador.
Fazendo a hipótese de que o controlador H(s) é do tipo proporcional, pede-se:
a) Para uma entrada em degrau de r(t) = A, e um distúrbio igual a d(t) = 0, calcule o erro
estacionário fornecido pelo sistema de controle de malha fechada.
b) Se o distúrbio for do tipo degrau d(t) = b, calcule o erro estacionário fornecido pelo
sistema de controle de malha fechada.