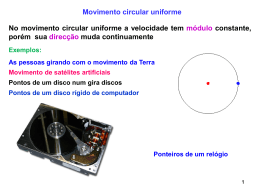
• Características gerais das ondas que se propagam em estruturas com secção transversal
uniforme.
x
z
ε2, μ2
ε1 , μ
ε1, μ1
diel. 1
diel. 2
y
e jk z z
Eqs. de Helmoltz
2
2
T E 
E  k12 E  0
~
~
z 2 ~
 2 E  k12 E  0
~
~
2
 E  k12 H  0
~
~
k1   11


~
~
2
T
H  k12  k 2
z H  0
~
~
2
T
E  k12  k 2
z E0
E x, E y , Ez
H x, H y , Hz
E x, E y , E z e H x, H y , H z
  E   j H e   H  j E
~
~
~
~

  jk z
z
Ex 

Ez
Hz 

jk

jk
Z
z
1 1



x

y
k12  k 2

z 
1

Ez
Hz 
Ey 

jk

jk
Z
z
1 1

2
2

y
x 
k1  k z 
1
Hx 
 k1  E z
Hz 
j

jk
z


Z

y

x
k12  k 2
1

z 
Hy 

k1  E z
Hz 

j

jk
z


Z

x

y
k12  k 2
1


z
1
1
k1   11 Z1 
1
1
• Geometria da secção transversal
do guia + soluções nas fronteiras
→
EH
~
~
a) Modos TM
• m=0, guias de planos paralelos
Ez  0
vf 
Hz  0

 c1
kz
ZT EM 
vg 
 k12  k 2z  0
 k z  k1 

c1

 c1
k z
Ex

 1
1
Hy
• A velocidade de fase, a velocidade de grupo e a impedância das ondas TEM são
independentes da frequência das ondas.
• Os modos TEM podem existir em guias de planos paralelos, cabos coaxiais e linhas
bipolares??.
• Os modos TEM não podem existir em guias de onda metálicos ocos, qualquer que seja a
sua secção transversal.
• Guia de planos paralelos
Tem fugas nas partes laterais do guia
• Guia de secção rectângular


2
T
E z  k12  k 2
z E z  0
2
T
H z  k12  k 2
z H z  0 M odos TE
M odos TM
2
2
2
T 

2
2
x
b
y
a
• Método de separação de variáveis
2
2
T
Fz  k c
F0
k c2  k12  k 2z 
F  X ( x ) y( y ) e  jk z z
1 d 2X
1 d2y
2

 kc
0
X dx 2
y dy 2
1 d 2X
 k2
x 0
X dx 2
1 d2y
 k2
y 0
y dy 2
2
2
k12  k 2
x  k y  kz
2
kc
z
y
x
Solução Geral:
X  A1 cos k x x   B1 sin k x x 



Y  A 2 cos k y y  B2 sin k y y

• As condições fronteiras nas paredes condutoras permitem determinar
E 0e H 0
~t
~n
Modos TE
A1, B1, A 2 eB 2
H z  X ( x ) Y ( y)e  jk z z


H z  A1 cos( k x x )  B1 sin( k x|x ) A 2 cos( k y y)  B2 sin( k y y)
 Em x  0 e x  a : E y  H x  0
 B1  0
k x a  m (m inteiro )
 Em y  0 e y  b : E x  H y  0
 B2  0
k y b  m (n inteiro )
H z  H z 0 cos( k x x ) cos( k y y)e  jk z z


kx  m
ky  n
a
a

Modos TM



E z  A1 cos( k x x )  B1 sin( k x|x ) A 2 cos( k y y)  B2 sin( k y y) e jk z z
 Em x  0, x  a , y  0, y  b : E z  0
 A1  0 k x a  m
A 2  0 k y b  n
E z  E z0 sin( k x x ) sin( k y y)e jk z z


kx  m
ky  n
a
a
Modos TEmn
H z  H z 0 cos( k x x ) cos( k y y) exp(  jk z z)
k k
H x  jH z 0 z x sin( k x x ) cos( k y y) exp(  jk z z)
k c2
H y  jH z 0
k zk y
k c2
E x  ZT E H y ,
cos( k x x ) sin( k y y) exp(  jk z z)
E x   ZT EH x ,
ZT E  Z1k1 / k z,
Modos TMmn
E z  E z0 sin( k x x ) sin( k y y) exp(  jk z z)
k k
E x   jE z 0 z x cos( k x x ) sin( k y y) exp(  jk z z)
k c2
E y  jE z 0
k zk y
k c2
sin( k x x ) cos( k y y) exp(  jk z z)
H x  E y / ZT M, H y  E x / ZT M,
ZT M  Z1K z / k1,
Características de propagação de modos
TEmn e TMmn
• A constante de propagação longitudinal só pode tomar valores discretos:
2
k zmn  k12  k cmn

k1 
c1
2
2
   
2
k cmn   m    m 

a

b
Frequência de corte
c
fcmn  1 k cmn
2
Os modos TEmn e TMmm são modos degenerados
Modo fundamental TE10
c
f c10  1
2a
H z  H z 0 cos( k x x )e jk z z
b
k
H x  jH z 0 z sin( k x x )e jk z z
kx
a>b
a
E y   ZT E H x
k
ZT E  Z1 1
kz
kx 

a
ky  0
Valor médio da energia transmitida por unidade de tempo
E .E
1
Pz   ~ T ~ T
2 ST zT
kc  k x
Guia rectagular
Modos TEmn , TMmn
z
x
kz 
b
y
a>b
 m  2  n  2 
2
 11  
 
 
a
b



 


a
• Indíce m – nº de meios ciclos do campo e.m. na direcção xx
• Indíce n – nº de meios ciclos do campo e.m. na direcção yy.
• Cada modo apresenta a sua impedância característica
Frequência de corte
c1  m 2  n 2
fcmn 
   
2 a
b
k
ZT E  Z1 1
kz
kz
ZT M  Z1
k1
Modo fundamental TE10
Guia rectagular
Modos TEmn , TMmn
z
x
kz 
b
y
a>b
 m  2  n  2 
2
 11  
 
 
a
b



 


a
• Indíce m – nº de meios ciclos do campo e.m. na direcção xx
• Indíce n – nº de meios ciclos do campo e.m. na direcção yy.
• Cada modo apresenta a sua impedância característica
Frequência de corte
c1  m 2  n 2
fcmn 
   
2 a
b
k
ZT E  Z1 1
kz
kz
ZT M  Z1
k1
Modo fundamental TE10
Modo fundamental TE10
Como a > b
2
2
c1  m   n 
fcmn 
   
2  a  b
c
fc10  1
2a
a


fc10  f  fc011   2 
b


• Guias em regime unimodal:
H z  H zo cosk x x e  jk z z
k
H x  jH zo z sin k x x e  jk z z
kx
fc01 
c
2b
a

fc10  f  fc20  2 
b

c 2 c
fc20  1  1
2 a a
a  2b  fc01
E y   Z T EH x
H z  H zo cosk x x  cost  k z z 
k
H x  H zo  z
 kx



 sin k x x  cos t  k z z  
2


k
H y  Z1H zo  1
 kx



 sin k x x  cos t  k z z  
2


E
~
Velocidade e Velocidade de grupo de fase
•
Velocidade de fase de uma onda plana com uma frequência angular ω
vf 
•
•


A velocidade de fase de ondas planas em meios sem perdas é independente da frequência.
Num meio dieléctrico com perdas
 
•
   
2

1   
 1  
 
8


 



 não é uma função linear de ω. vf depende da frequência.
Dispersão – fenómeno de dispersão do sinal originado pela dependência de vp com a
frequência
Sinal com duas frequências ligeiramente diferentes ω0  Δω e ω0  Δω
Δω  ω0 
co s0   t  0   Z 
 E 0 co s 0   t  0    Z
E z, t   E 0 co s  t   z  co s 0 t   0 z 
E Z, t   E 0
•
como Δ ω << ω0 a expressão representa uma onda que oscila rapidamente à frequência
ω0 e uma amplitude (envelope) que oscila lentamente à frequência Δω.
•
A onda dentro do envelope propaga-se à velocidade de fase
0 t  0 z  ct e
vp 
0
0
t   z   ct e
• A velocidade para seguir um ponto do envelope
dt   z   0


  0 
vg 