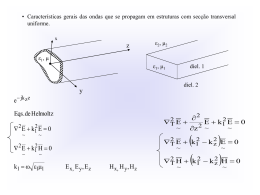
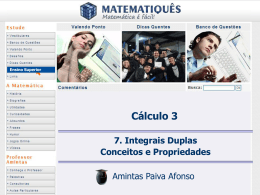

v0
Analisamos o movimento
dimensões separadamente
em
cada
uma
das
Componentes da velocidade inicial

v0

ey



v0  v0 xex  v0 y ey
cos 0 
0

ex
v0 x
v0
sin 0 
As componentes iniciais
são
v0 x  v0 cos 0
v0 y
v0
x e y da velocidade
v0 y  v0 sin 0
1
Duas esferas largadas simultaneamente
2
Fotografia estroboscópica de duas esferas largadas simultaneamente
As duas esferas são jogadas sob
a acção da gravidade
A esfera rosa é solta  v0y = 0
(queda livre)
A esfera amarela tem velocidade
inicial horizontal v0x
A cada instante as esferas têm a
mesma altura
As duas esferas chegam ao
mesmo tempo no solo
3
Exemplo:
Quando um avião em deslocamento horizontal com velocidade constante
deixa cair um pacote com medicamentos para refugiados em terra, a
trajectória do pacote vista pelo piloto é igual à trajectória vista pelos
refugiados?
Não. O piloto verá o pacote descrever
uma trajectória rectilínea vertical:
Os refugiados verão o pacote descrever um
movimento horizontal uniforme e um vertical
uniformemente acelerado, a visão será de uma
trajectória parabólica:
4
Visão do piloto e visão dos refugiados
5
Diagrama do movimento de um projéctil
g
Movimento uniformemente variado
Movimento rectilíneo uniforme
6
Exemplo do movimento de um projéctil
7
EQUAÇÕES DE MOVIMENTO DO PROJÉCTIL
Movimento rectilíneo uniforme na horizontal (MRU)
Componente horizontal da velocidade
v x  v0 x  v0 cos 0  constante
Componente horizontal da posição
x  x0 x  v0 x t  x0 x  v0 cos 0 t
Movimento uniformemente variado na vertical (MRUV)
Componente vertical da velocidade
Componente vertical da posição
v y  voy  gt  v0 sin 0  gt
y  y0  v0 y t 
1 2
1
gt  y0  v0 sin 0t  gt 2
2
2
8
Alcance e altura máxima dum projéctil
ALTURA MÁXIMA
vy  0
O tempo para atingir a altura máxima y=h
(quando v y  0 ) :

v0
v y  v0 y  gt
v y  v0 y  gth  v0 sin  0  gth
0  v0 sin  0  gt h 
gt h  v0 sin  0 
0
v0 sin  0
th 
g
Substituindo th na outra expressão
y  y0  v0 sin  0t 
1 2
1
gt  h  v0 sin  0t h  gt h2 
2
2
 v0 sin  0  1  v0 sin  0  v0 sin  0 2
  g 
 
h  v0 sin  0 
2g
 g  2  g 
2

(y=h e y0=0)
v02 sin 2  0
h
2g
9
ALCANCE
v0 y  0

v0
R é o alcance - distância horizontal
percorrida pela partícula até chegar à
altura inicial
O movimento é simétrico 
a partícula
leva um tempo th para subir e o mesmo
tempo th para cair ao mesmo nível
Portanto o tempo para percorrer R é
t  2th  2 v0 sin  0
g
0
x  x0 x  v0 x t  x0 x  v0 cos 0 t
R  v0 x (2th )  v0cos0 (2th )
 2v0 sin  0 

R  v0 cos  0 
g



v02 sin 20
R
g
10
Um projéctil lançado da origem com uma velocidade escalar inicial de
para vários ângulos  0
50 m/s
Alcance máximo Rmáx
R
v2
0
g
sin 2 0
sin 20 é máximo quando for  1
O que acontece quando
 0  45 o
20   / 2
Rmax 
v 20
g
Os ângulos complementares (somam 90 graus) dão origem ao mesmo valor de R
11
Exemplo 11. Um canhão atira esferas com velocidade v0 = 100 m/s. a) Determine o
alcance máximo da esfera. b) Mostre que existem dois ângulos possíveis para atingir um
alvo à uma distância d = 800 m, menor que a distância máxima.
a) Determine o alcance máximo da esfera
2
v0
(100 m/s) 2

 1020 m
Rmáx=
2
g
9.8 m/s
b) Mostre que existem dois ângulos possíveis para atingir um alvo à uma distância d =
800 m, menor que a distância máxima
R
v sin 2 0
g
2
0
2
, mas
v0
 Rmáx
g
. Substituindo, fica
R  Rmáx sin 20
assim
sin 2 0 
R
800 m

 0.784
Rmáx 1020m
201  52o  01  26o
e o ângulo complementar
 02  90o -26o  64o
12
Movimento circular uniforme
No movimento circular uniforme a velocidade tem módulo constante,
porém sua direcção muda continuamente
Exemplos:
As pessoas girando com o movimento da Terra
Movimento de satélites artificiais
Pontos de um disco num gira discos
Pontos de um disco rígido de computador
Ponteiros de um relógio
13
Movimento circular uniforme  MCU
y

ey

r


ex
Para descrever o MCU utilizamos as coordenadas polares
x
r
e 
y

e
r sin y

r
Vector posição


ex
r cos 
x



r  r cos e x r sin  ey
onde

r r
14
O arco sobre a trajectória que subentende um ângulo
y
r

é:
s  r
S

x
ds
r

d
s
O arco descrito em
d é dado por
ds  r d
x
15
No movimento circular uniforme 
O vector velocidade é sempre tangente à
trajectória da partícula e é perpendicular
ao raio da trajectória

v

ac
r
B

v

ac
A
Demonstraremos que
• A aceleração centrípeta aponta para o centro do círculo
• A aceleração centrípeta é responsável pela mudança da direcção da velocidade
16
No movimento circular uniforme a velocidade angular é constante


t
A unidade da velocidade angular é
rad s 1
O movimento circular é um movimento periódico
O tempo de uma volta completa é o período T

o tempo que demora para descrever um ângulo de
A velocidade angular é

2
T
ou
2
  2f onde f é a frequência
A unidade da frequência no SI é o hertz (Hz)
17
y



r  r cos e x r sin  ey
A velocidade da partícula

v
é a
derivada em ordem ao tempo de

r

 dr 
d   
d
v
   r sin 
e

r
cos

 x 
dt 
dt 
dt

mas

ey

e y

d

dt

r

v


ex
x
  v  r sin 
x
 v vy 
v y  r cos


vx



v   r sin  e x r cos ey 



O módulo da velocidade é v  v    r sin  e x  r cos  e y   r
porque
2 2
2
2 2
2
2 2
2
2
v 2   2  r sin    2 (r cos ) 2   r sin    r cos    r (sin   cos  )
2
 v  r
Relaciona a velocidade angular

velocidade linear
v
18
O valor absoluto da velocidade linear não varia mas a direcção varia
Como
v  r ,  também não é constante.
O movimento circular uniforme é acelerado e a única função da aceleração é mudar a



v   r sin  e x r cos ey 

 dv d


a

 r sin  e x r cos  e y
dt dt
direcção da velocidade
A aceleração é


d   
d   
    r cos
 e x   r sin 
 ey 
dt
dt


 


   r 
2




(r  r cos e x r sin  ey )
Observe que a direcção da aceleração tem
sentido inverso ao do vector posição 
Está dirigida para o centro da circunferência e
por esse motivo chama-se aceleração
centrípeta
É a aceleração centrípeta que faz variar o
vector velocidade
19
O módulo da aceleração centrípeta é

v

ac


2
ac    r
B

v

ac
A
como
v  r
ac   r
2
2
v
ac 
r
20
Observe a animação abaixo. O carro se move com velocidade linear constante.
Em qual das curvas a aceleração centrípeta é maior?
v2
ac 1 
r
v2
ac 2 
2r
21