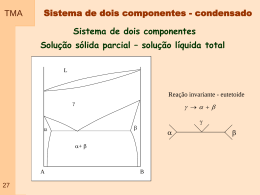
TMA
As Relações de Maxwell
dU  TdS  PdV
Matemática:
dH  TdS  VdP
f  f ( x , y)
dA  SdT  PdV
dG  SdT  VdP
01
df  gdx  hdy
Se e somente se,
 g   h 
    
 y  x  x  y
 T 
 P 

   
 V S
 S  V
 S   P 

  
 V T  T  V
 T   V 
  

 P S  S  P
 S 
 V 
   

 P T
 T  P
TMA
EXERCICIO
Considere um bloco de ferro puro a 298 K.:
a) Qual o volume molar do ferro?
b) Determine uma equação para a variação da entropia com
a pressão a temperatura constante para um sólido,
expressa em termos de parâmetros mensuráveis, como
os apresentados abaixo.
c) Sabendo que a entropia molar do ferro a 298 K e 1 atm
está disponível em handbooks, e é de 27,28 J/Kmol, qual
o valor da entropia molar do ferro a 298 K e 100 atm.
Qual o erro percentual assumido se considerarmos a
entropia como constante neste intervalo de pressão.
Dados:
Cp = 24 J/Kmol
Compressibilidade = 6x10-7 /atm
Coeficiente de expansão térmica linear = 15x10-6 /oC
Densidade = 7,87 g/cm3
Peso molecular = 55,85 g/mol
01a
TMA
Outras Relações importantes
dG  SdT  VdP
dV  VdT  VdP 
dU  Cp  PVdT  VP  TdP
dH  CpdT  V1  TdP
dA  S  PVdT  PVdP
 Cp

dS   dT  VdP 
 T

02
Energia Livre de Helmholtz - Gibbs
TMA
Sistema em equilíbrio térmico com as vizinhanças–temperatura
T
Ocorre mudança de estado com transferência de calor
Processo espontâneodS
sis
 ds viz  0
dq
dS 
0
T
Volume Constante
032
Pressão Constante
dSU,V  0
dSH,P  0
dUS,V  0
dHS,P  0
dU  TdS  0
dH  TdS  0
TMA
04
Energia Livre de Helmholtz - Gibbs
dU  TdS  0
dH  TdS  0
dA T
dG T
dAT,V  0
dG T,P  0
Energia Livre de Gibbs
TMA
Relação entre energia de Gibbs e temperatura a pressão
constante
 G 

  S
 T  P
05
Energia Livre de Gibbs
TMA
 G 

  S
 T  P
GH
 G 



T
 T  P
   G 
H
      2
T
 T  T   P
06
   G  
H
 




2

T
T
T
 P
 
G  H  TS
GH
 S
T
G H
 G 




 T  P T T
Equação de Gibbs - Helmholtz
Energia Livre de Gibbs
TMA
Relação entre energia de Gibbs e pressão a temperatura
constante
 G 

 V
 P T
07
Energia Livre de Gibbs
TMA
Relação entre energia de Gibbs e pressão a temperatura
constante
Pf
 G 

 V
 P T
G   VdP
dG  VdP
Pi
Pf
G Pf   G Pi    VdP
Pi
Sólidos e liquidos
Gás ideal
08
GPf   GPi   VP
 Pf
GPf   G Pi   nRT Ln
 Pi
Gás ideal-Pi= Ppadrão



P 
GPf   G   nRT Ln f 
P 
TMA
09
TMA
Potencial Químico
É uma medida de quanto varia a energia livre de um sistema
quando se adiciona a ele uma quantidade de substancia
Considera a possibilidade de transferência de massa
 G 


 n  T ,P
dU  q  W  ndUn
Sistema contendo dois componentes
 G 
 G 


 B  
dU  q  W  n AdU A  n BdU B  A  
 n B  n iBT ,P
 n A  n iA T ,P
Sistema contendo n componentes
10
dU  q  W   nidUi
 G 

 i  
 n i  n i jT ,P
Potencial Químico
TMA
 G 

  Gm
 n T,P
 Pf 
GPf   G  nRT Ln  
P 

 Pf 
Pf     RT Ln  
P 

Pf     RT LnPf 
11
Fugacidade
TMA
Fugacidade esta associado com quanto o comportamento de
um sistema foge da idealidade
A
dependência
químico
Gás Ideal
e
 Pf 
Pf     RT Ln  
P 

Gás Real
 f 
Pf     RT Ln  
f 

Medida da tendência a escapar do
comportamento ideal
12
a
pressão
mesma
pressão
potencial
deve
ser
adaptada no caso de gases reais
PV  nRT
Tem
entre
dimensão
que
a
Estado Padrão
TMA
O estado padrão de um gás real é um estado hipotético em
que o gás está na pressão po e tem o comportamento de gás
perfeito
Relação entre fugacidade e pressão
f  p
 P 
    RT ln    RT ln 
P 

132
TMA
14
Relação entre fugacidade e pressão
TMA
Atividade
Definida com base na fugacidade.
É a razão entre a fugacidade do material em relação a
fugacidade no estado padrão, em uma mesma temperatura.
O estado padrão para o gás é o material puro na pressão de 1
bar. Para líquidos e sólidos é considerado o material puro na
pressão de 1 atm
 f 
Pf     nRT Ln  
f 

15
TMA
Equilíbrio
Segunda lei da termodinâmica: a entropia do universo tende
a permanecer constante ou a aumentar.
Para um sistema isolado a entropia deste deve aumentar ou
permanecer constante;
Questão 1 : Existe um máximo para a entropia?
Questão 2 : O que e equilíbrio?
Existe uma relação entre equilíbrio e forca motriz
No equilíbrio as propriedades macroscópicas do sistema
permanecem constantes tornando-se independentes do
tempo
Quando nos aproximamos do equilíbrio a taxa de aumento
da entropia diminui
16
TMA
Equilíbrio
Em um sistema isolado, a entropia e máxima no ponto
de equilíbrio
Equilibrio Térmico
A temperatura de um sistema e uma medida do potencial ou
intensidade de calor do sistema.
E uma medida da tendencia de transferencia de calor no
sistema.
Duas partes do sistema com temperaturas diferentes (
gradiente de temperatura) possuem uma forca motriz para o
fluxo de calor.
O equilibrio termico e atingido quando nao existe gradiente
de temperatura no sistema.
17
TMA
Equilíbrio
Equilibrio e Pressão
A pressao de um sistema e uma medida da tendencia de
movimento;
Se a pressao exercida por uma fase sobre o sistema, e maior
que o de outras, existe uma tendencia de expansao de uma
fase em relacao a outra;
O equilibrio ocorre quando a pressao em todo o sistema e
constante
Equilíbrio e Potencial Químico
18
O potencial quimico de um componente em uma fase e uma
medida da tendencia de difusao deste componente para
outra fase.
se os potenciais quimicos de um componente de diferentes
fases do sistema forem diferentes, existira uma tendencia a
difusao deste componente de uma fase para outra
O equilibrio ocorrera quando o compoente estiver distribuido
de tal forma entre as fases de forma a que todas tenham o
mesmo potencial quimico
Equilíbrio
TMA
-Temperatura constante (equilíbrio térmicos)
-Pressão constante (equilíbrio mecânico)
-Potencial químico constante (equilíbrio químico)
-Mínima
-Mínima
-Mínima
-Máxima
19
entalpia
energia livre de Helmholtz
energia livre de Gibbs
entropia
Exemplo de equilíbrio – H2O
TMA
A 1 atm água e gelo estão em equilíbrio a 0 C, quando a
variação de energia livre de Gibbs molar e mínima.
Se calor e fornecido e gelo e convertido e água líquida o
equilíbrio não é alterado pois o potencial químico das duas
fases e o mesmo
Pressão constante
Pressão constante
Líq
uid
o
G
20
T
Tm
0
G(sl)
Sól
ido
T
Tm
G=H-TS
TMA
30
TS (kJ)
28
H (kJ) 4
(l)
H 2O
2
26
24
0
)
O (l
H2
22
-2
20
-4
H 2O (s)
-6
18
16
O (s)
H2
-8
14
250
275
T (K)
300
325
350
12
10
250
275
300
T (K)
21
325
350
H(s-l)=Tm  S
TMA
(s-l)
(kJ)10
9
8
7
6
5
4
1
0
-1
250
275
300
T(K)
22
325
350
TMA
Pressão -temperatura
Temperatura constante
Temperatura constante 0 C
G
T
G
0,0075oC
0,006 atm
P
1 atm
P
0oC, 1atm
23