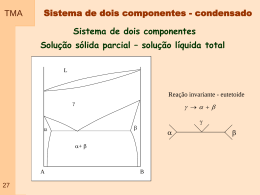
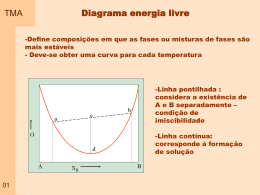
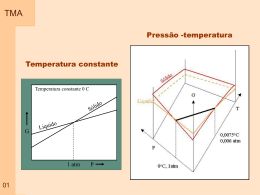
Misturas Simples
TMA
Diferenciação entre substâncias Puras e misturas simples
Assume-se em geral que em misturas simples não existe reação
Termodinamicamente
Energia associada com a mistura apenas e com as interações
entre as substâncias, que não envolvam reação
Misturas de dois componentes A e B
X A  XB 1
Para gases ideais
p A  pB   X A  X B  p  p
01
Volume Parcial Molar
TMA
Adiciona 1 mol
de H2O
Adiciona 1 mol
de H2O
Volume aumenta
de 18 cm3mol-1
Volume aumenta
de 14 cm3mol-1
Volume Molar da
H2O : 18 cm3mol-1
Volume Molar da
H2O : 14 cm3mol-1
A diferença de aumento de volume depende do tipo de molécula
que envolvem as moléculas de água adicionadas
Definição : Volume molar da substância A em uma mistura é a
variação de volume por mol de A adicionada a um grande volume
de mistura.
02
Volume Parcial Molar – representação
TMA
T= 25 oC
Volume Parcial Molar da água
Etanol
Água
Percentual de etanol
 V 
 V 


dV  
dnH 2O  
dne tanol
 nH O 

n
 e tanol  p,T ,nH2O
2

 p,T ,ne tan ol
03
Volume Parcial Molar do etanol
VH 2O
 V 


 nH O 
2

 p ,T ,ne tan ol
 V
Ve tanol  
 ne tanol


 p ,T ,nH2O
 V 

VJ  

 nJ p,T ,n
Onde n´ significa todos
os outros componentes
presentes
TMA
Volume Parcial Molar – cont.
Definição : O volume parcial molar ( que pode ser positivo ou
negativo) é o coeficiente angular da curva do volume total da
amostra pelo numero de moles de um dos componentes, quando
são mantidos constantes a Pressão; a temperatura; e a
quantidades dos outros componentes
Misturas de dois componentes A e B
 V 

VA  
 n A  p ,T ,nB
Qual o
significado do
volume parcial
molar negativo ?
 V 
 V 


dV  
dnA  
dnB


n

n
 A p,T ,nB
 B p,T,nA
O que acontece
se a Temperatura
variar?
dV  VAdnA  VB dnB
V  VAnA  VB nB
04
Quantidade de A, (nA)
TMA
Energia Livre de Gibbs Parcial Molar
Definição : O conceito de quantidade parcial molar pode ser
aplicada a qualquer variável extensiva, que seja função de
estado. Ex. Energia livre de Gibbs parcial molar.
Complemento: Para uma substância Pura o potencial químico
representa a Energia Livre de Gibbs Molar. Para uma substância
em uma mistura, o potencial químico se define como a Energia
Livre de Gibbs Parcial Molar.
 G 

 J  
 nJ  p ,T ,n
Onde n´ significa todos
os outros componentes
presentes
Definição: O potencial químico é o coeficiente angular da curva
de Energia Livre de Gibbs em função do número de moles do
componente J, quando são mantidos constantes a Pressão; a
05
temperatura; e a quantidades dos outros componentes.
TMA
Energia Livre de Gibbs Parcial Molar - cont
Misturas de dois componentes A e B
dG  Vdp  SdT
 G 
 G 


dG  
dnA  
dnB
 n A  p ,T ,nB
 nB  p ,T ,n A
Se não há variação de massa
Se P e T são constantes com variação de
massa (nJ)
 G 
 G 


dG  Vdp  SdT  
dnA  
dnB

n

n
 A  p ,T ,nB
 B  p ,T ,n A
06
Geral – Equação fundamental geral
da Termodinâmica
Energia Livre de Gibbs Parcial Molar - cont
TMA
Definição : O potencial químico mostra como as grandezas
termodinâmicas extensivas A, H, U e G dependem da
composição
 G 
 U 
 H 
 A 




 J  
 
 
 

n

n

n

n
 J  p ,T ,n  J  S ,V ,n  J  S , p ,n  J T ,V ,n
´
´
´
´
 G 
 G 


dG  Vdp  SdT  
dnA  
dnB
 n A  p ,T ,nB
 nB  p ,T ,n A
dG  Vdp  SdT   AdnA  B dnB
Se P e T = Constante
dG   AdnA  B dnB
Equação de Gibbs-Duhem
nAd A  nB dB  0
d A  
07
 n d
J
J
J
nB
d B
nA
0
Função de estado
dG   AdnA  B dnB  nAd A  nB dB
?
G   AnA  B nB
dG   AdnA  B dnB
Energia Livre de Gibbs de misturas
TMA
Misturas de dois componentes A e B
A
B
G   AnA  B nB
Se P e T = Constante
Exemplo clássico : Mistura de dois
gases ideais
A
08
Inicial
(gases separados)
Final
(Mistura de gases)
(Sem reação)
Gi
Gf
T, P constante
B
G=Gf- Gi
TMA
misG  nRTXA lnXA   XB lnXB 
09
 mis H  0
  G 
 misS   mis 
 T P,nA ,nB
misS  nRXA lnXA   XB lnXB 
Potencial Químico de líquidos
TMA

pA 

 A    RT  Ln  
p 


A
Potencial químico gás puro
Para falarmos em fases condensadas e Importante a relação
entre fase condensada e pressão de vapor
T
re
10
Átomos de A líquido
rc
Na
condição
de
equilíbrio
existe um equilíbrio entre
evaporar e condensar.
Existe um equilíbrio entre a
taxa de evaporação e taxa de
condensação
No
equilíbrio
define-se
a
pressão de vapor
TMA
Taxa de evaporação – É função da força de ligação entre
átomos. Quanto maior a força de ligação menor a taxa de
evaporação.
Taxa de condensação – depende da concentração de átomos
de A no estado vapor que se chocam com a superfície do
líquido por unidade de tempo.
Esta taxa de condensação é proporcional à pressão parcial
T
T
re
rc
Átomos de A líquido
11
re
rc
Átomos de B líquido
T
re
rc
O que acontece se átomos
de A e B forem misturados?
Potencial Químico de líquidos
TMA


 A   A  RT  n
pA 

   A  RT n p A 
1 
O potencial químico de um líquido
puro será dado por
*


p
 *A   A  RT  n A 
1 

  A  RT n p *A
  
O potencial químico do liquido A em
uma mistura de dois líquidos A e B
 pA 
 A    RT  n * 
 pA 
*
A
12
Potencial químico gás
puro
Lei de Raoult
TMA
François Raoult – Químico Frances

pA 

 A    RT  Ln * 
pA 

  *A  RT LnX A 
*
A
13
Pressão Total
Pressão
Para
misturas
de
líquidos
similares a relação da pressão
parcial de vapor de cada
componente da mistura em
relação à pressão de vapor do
componente
puro,
é
aproximadamente
igual
à
fração
molar
do
liquido
presente na mistura.
pA
 XA
*
pA
Pressão
Parcial de A
Pressão
Parcial de B
Fração Molar de A
Lei de Raoult - interpretação
TMA
-Considerando
a taxa de evaporação das
moléculas
-A presença de um segundo componente
interfere na remoção de moléculas do
meio líquido mas não impedem a
condensação.
-Taxa de vaporização
T axade vaporização  kXA
-Taxa de condensação
T axade condensação  k´pA
-No equilíbrio
T axade condensação  T axade evaporação
kX A  k ´ pA
14
kX A
pA  ´
k
Para um líquido puro XA  1
k
p  ´
k
*
A
pA
 XA
*
pA
TMA
Lei de Raoult – Afastamento do comportamento
Comportamento Ideal
15
Comportamento Real
TMA
Lei de Raoult – Afastamento do comportamento
Característico de misturas de líquidos que apresentam
diferenças químicas significativas
Quando a solução é muito diluída o solvente comporta-se como
ideal
Quando em soluções diluídas o soluto apresenta pressão de
vapor definida por uma constante de proporcionalidade
Lei de Henry
16
Lei de Henry
TMA
Soluções reais, com baixas
concentrações, a pressão de
vapor do soluto é proporcional
a
fração
molar,
mas
a
constante de proporcionalidade
não é a pressão de vapor do
componente puro.
pA
 XA
*
pA
17
Pressão
William Henry – Químico Inglês
pA
 XA
kB
São conhecidas como soluções
ideais diluídas onde solvente é
um líquido puro, ligeiramente
modificado. O soluto presente
em baixas concentrações
Fração Molar de A
TMA
- Se as ligações A-B forem mais fortes que A-A e B-B
T
re
re
Numero de ligaçoes A-A diminuem
Numero de ligações A-B aumentam
Taxa de evaporação de A diminui
se XA diminui
T
re
Numero de ligaçoes B-B diminuem
Numero de ligações A-B aumentam
Taxa de evaporação de B diminui
se XB diminui
Lei de Henry – define a dependência entre taxa de evaporação e
composição da mistura
18
PAo
0
19
Pressão de vapor
Pressão de vapor
TMA
Xa
0
1
Se A-B maior que A-A e B-B
re´(A)< re(A)
Linha de Henry acima da
Raoult
PAo
de
Xa
1
Se A-B menor que A-A e B-B
re´(A)> re(A)
Linha de Henry abaixo da de
Raoult
TMA
Energia Livre de Gibbs de misturas
Misturas de dois componentes A e B
Solução ideais – que segue a lei de Raoult
20
TMA
Energia Livre de Gibbs soluções reais
O que foi considerado até agora:
-Mistura de gases ideais :
não existe interação entre componentes
-mistura de líquidos ideal :
existe interação entre moléculas mas, em média as
forças de interação entre A e B são semelhantes às
interações A-A e B-B.
-Soluções reais:
as interações entre A-A, A-B e B-B são diferentes
O tipo de interações em soluções reais definem se a mistura
resultará em:
- miscibilidade total
- Imiscibilidade total
- miscibilidade parcial
21
TMA
Energia Livre de Gibbs soluções reais
Para soluções reais usa-se a função excesso XE
Exemplo: SE é a diferença entre a variação de entropia observada
e a variação de entropia se a solução fosse ideal
22
TMA
Energia Livre de Gibbs soluções reais
Exemplo: Função modelo para entalpia
H E  mis H  mis H ideal
H E  nRTX A X B  nwX A X B

Medida da força de interação A-B
Endotérmico
Exotérmico
23
TMA
Energia Livre de Gibbs soluções reais
Exemplo: Função para Energia Livre de Gibbs
mix G  nRT X A ln aA  X B ln aB 
mixG  nRT X A ln X A  X B ln X B  X A X B 
Para  > 2 pode gerar
separação de fase
24
?
Atividade em solução
A atividade de um componente em qualquer estado em uma temperatura T é
definido como a relação entre a fugacidade da substancia do estado e a
fugacidade no estado de padrão.
Atividadede A  a i 
G  RTXA ln XA  XB ln XB 
G  RTXA ln XA  XB ln XB 
G  RTXA ln a A  XB ln a B 
fi
f io
Solução de gases ideais
Solução de fases condensadas ideais
Solução de fases condensadas reais
Para uma solução real:
•a atividade de A na solução não pode ser considerada igual a fração molar
•Existe um fator de aproximação chamado de coeficiente de atividade 
•Este coeficiente é a relação entre a atividade e a fração molar

G  RTXA ln a A  XB ln a B 
• Pode ser maior ou menor que 1.
•Se for maior que 1 diz-se que a
aA
XA
Determinar o coeficiente de atividade
é
importante
para
determinar
a
variação da energia livre
solução apresenta deslocamento positivo em
relação à lei de Raoult.
•Se for igual a 1 a solução comporta-se como solução ideal
•Se for menor que 1 diz-se que a solução apresenta deslocamento negativo em
relação à lei de Raoult.
•H de mistura não é zero
•O aumento da temperatura tende a aproximar o comportamento de misturas do
comportamento ideal.
•Se >1 o aumento da temperatura tende a diminuir o valor de 
•Se <1 o aumento da temperatura tende a aumentar o valor de 
•Se H de mistura é negativo – processo exotérmico – tendência para
formação de compostos
•Se H de mistura é positivo – processo endotérmico – tendência para
formação de separação de fases
Variação de energia livre – Diagrama de fases
-Sistema isobárico
-Temperatura e composição variando
-A fase existente será aquela que apresenta menor energia livre
-Existe uma relação quantitativa de fases que , para uma determinada temperatura e
composição correspondem a mínima energia
c
a
b
G
d
A
XB
B
o
a
p
n
G
G
b
r
m
A
s
q
XB
B
Ni
Cu
Ni
Cu
Solução - Líquido
Solução Sólida
Cu
Zn
Solução sólida
Zn Cu
Composto de Cu Zn
O que define a solubilidade
Solução em cobre