Funções
1. Interpretação de Gráficos
O gráfico representa a viagem da Joana num dia em que resolveu
visitar uns amigos
Distância
( Km)
Tempo
(horas)
Voltar
Ana Arromba - Instituto de Almalaguês
Manuela Pedro - Instituto de Almalaguês
Paula Curto - Escola Básica 2,3/Secundária de
Condeixa-a-Nova
Circulo de Estudos
Desenvolvimento do Programa de 10º ano de
Matemática B para o Ensino Secundário
Janeiro e Maio 2002
Escola Secundária Martinho Árias
Funções
1. Interpretação de Gráficos
 A que distância de casa estava a Joana quando
efectuou a primeira paragem?
A Joana estava a 10m de casa.
 Durante a viagem, qual foi a distância máxima que a
separou de casa?
A distância máxima que a separou de casa foi 15m.
 Quanto tempo demorou a viagem?
A viagem demorou 3h30m.
 Quanto tempo esteve parada a Joana?
A Joana esteve parada 1h30m.
 A que horas chegou a Joana a casa?
A Joana chegou ás 3h30m.
Voltar
Funções
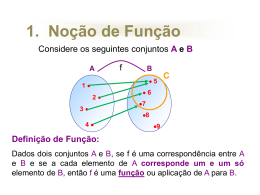
1. Noção de Função
Considera os seguintes conjuntos A e B
B
f
A
C
5
1
2
3
4
6
7
8
9
Definição de Função:
Dados dois conjuntos A e B, se f é uma correspondência entre
A e B e se a cada elemento de A corresponde um e um só
elemento de B, então f é uma função ou aplicação de A para B.
Voltar
Funções
1. Noção de Função
•A esta correspondência chama-se _________.
função
Domínio
•Ao conjunto A chamamos conjunto de partida ou _________________
e representa-se por ______.
Df = {
}
1, 2, 3, 4
D
f
•A todo o elemento de A chamamos _____________.
Objectos
•Ao conjunto B chamamos _______________________
Conjunto de Chegada da função.
Conjunto de chegada de f = {
5, 6, 7, 8, 9
}
•A todo o elemento de B ao qual corresponde um elemento de A
chamamos ___________.
imagem
Estabelece o conjunto C formado pelas imagens dos elementos de A
• Ao conjunto C chamamos ______________
contradomínio da função e representa-se
por
D’f
D’f = {
5, 6, 7
}
Voltar
Funções
1. Noção de Função
Simboliza-se do seguinte modo:
f: A
x
B
y=f(x)
• x é variável independente e y a variável dependente
• Ao conjunto A chamamos Domínio e representa-se por Df
• Ao conjunto B chamamos Conjunto de Chegada
• Ao conjunto das imagens chama-se Contradomínio da função e
representa-se por D‘f
• A cada objecto x corresponde uma e uma só imagem y=f(x);
Funções
1. Interpretação de diagramas
Exemplo 1:
A correspondência não é uma função porque o objecto 1 tem duas
imagens, 4 e 5, logo mais do que uma imagem.
Exemplo 2:
A correspondência não é uma função porque o objecto 2 não tem
imagens.
Funções
2. Representação gráfica de uma Função
Num determinado dia registaram-se as temperaturas de ar na cidade de
Aveiro, de hora a hora e, a partir delas, elaborou-se o gráfico das temperaturas
em função da hora do dia.
Temperatura
ºC
Horas
Indique:
• o domínio;
1
• o contradomínio;
• os intervalos de tempo onde a
0;24]
2
-3;6]
• as horas do dia em que se registou
a temperatura 0ºC
3
4
temperatura: - é positiva; - é negativa;
• os intervalos onde a temperatura: aumenta; -aumenta e é positiva; 5
diminui; - diminui e é positiva; - é
constante;
Funções
2. Representação gráfica de uma Função
• Como averiguar se se trata de uma função
Um gráfico de uma função só pode ser intersectado no
máximo uma vez por uma qualquer recta vertical.
Não se trata de uma
representação de uma
função
Trata-se de uma representação de uma
função
Funções
Interpretação gráfica do domínio
Domínio
O domínio de uma função obtém-se projectando o seu gráfico
sobre o eixo dos xx
Voltar
Funções
Interpretação gráfica do Contradomínio
Contradomínio
O Contradomínio de uma função obtém-se projectando o seu
gráfico sobre o eixo dos yy
Voltar
Funções
3. Noções gerais de uma função
• Zeros de uma função
Definição: Zero de uma função é todo o
objecto que tem imagem nula.
DDeterminação dos zeros de uma função:
Graficamente
Averiguar as abcissas dos pontos do gráfico para
os quais o gráfico da função intersecta o
eixo das abcissas ( xx )
Analiticamente
Determinar os valores de x para os quais f(x)=0
isto é, x: f (x)=0
zeros
Voltar
Funções
3. Noções gerais de uma função
• Sinal de uma função
Definição : Seja f uma função de domínio D, dizemos que :
- f é positiva em I (I D) se e só se f(x) > 0, para todo o xI.
- f é negativa em I (I D) se e só se f(x) < 0, para todo o xI.
DDeterminação do sinal de uma função:
Graficamente
-A função é positiva para todos os valores de x cujas
imagens estão acima do eixo das abcissas.
-A função é negativa para todos os valores de x
cujas imagens estão abaixo do eixo das abcissas.
f(x) >0
f(x) < 0
Voltar
Funções
Noções gerais de uma função
• Monotonia de uma função
f(b)
g(b)
g
g(b)
f(b)
g
f
f
g(a)
f(a)
f(a)
g(a)
O
a
b
O
a
b
a
A função f é crescente
num intervalo E.
A função g é decrescente
num intervalo E.
b
A função f é
estritamente crescente
num intervalo E.
a
b
A função g é estritamente
decrescente num intervalo
E.
Definição : Diz-se que f é crescente / estritamente crescente em EDf se para todos os
números reais a e b pertencentes a E, se a < b, então f(a)f(b) / se a < b, então f(a)< f(b).
Definição : Diz-se que g é decrescente / estritamente decrescente em EDf se para
todos os números reais a e b pertencentes a E, se a < b então g(a)  g(b) / se a < b, então
g(a)>g(b).
Definição : Uma função crescente ou decrescente diz-se monótona.
Observação: Uma função constante é considerada crescente e decrescente.
Voltar
Funções
Noções gerais de uma função
• Monotonia de uma função
Definição : Seja f uma função de domínio D.
f(a) é um máximo absoluto de f se, para todo o x pertencente a D, f(a)  f(x)
f(b) é um mínimo absoluto de f se, para todo o x pertencente a D, f(b) f(x)
Definição : Seja f uma função de domínio D.
f(a) é um máximo relativo de f se existir um intervalo aberto E contendo a tal que
f(a)  f(x), qualquer que seja o x  E  D
f(b) é um mínimo relativo de f se existir um intervalo aberto E contendo a tal que
f(b) f(x), qualquer que seja o x  E  D
Definição : Aos valores do domínio a que correspondem os máximos / mínimos relativos da
função chamam-se maximizantes / minimizantes
Voltar
Funções
Noções gerais de uma função
• Injectividade de uma função
FDefinição : Uma função f é
injectiva num intervalo EDf se
para dois valores quaisquer de E,
x1 e x2, se x1  x2 então f(x1) 
f(x2).
Definição : Uma função f é não
injectiva num intervalo EDf se
existem
pelo
menos
dois
objectos distintos com a mesma
imagem.
Voltar
Funções
Noções gerais de uma função
• Injectividade de uma função
Graficamente
Vê-se que uma função é não injectiva se existir pelo menos uma recta
horizontal que intersecte o gráfico da função em mais do que um ponto.
f é função injectiva
f é função não injectiva
Funções
Noções gerais de uma função
• Sobrejectividade de uma função
FDefinição : Uma função g é
sobrejectiva
se
o
seu
contradomínio coincide com o
conjunto de chegada.
g é sobrejectiva
f é não sobrejectiva
Funções
Noções gerais de uma função
• Taxa de Variação Média
A taxa de variação média
(t.v.m) entre a e b traduz a
f(b)
rapidez de variação da função
e obtém-se dividindo a
variação da função pela f(a)
amplitude do intervalo, isto é:
f
b-a
f(b) - f(a)
t.v.m. =
[a, b]
a
b-a
f(b)-f(a)
b
Funções
Noções gerais de uma função
• Observações
• se a função é crescente a taxa de variação média é positiva
nesse intervalo
• se a função é decrescente num dado intervalo então a taxa de
variação média é negativa nesse intervalo.
• se a função é constante num dado intervalo então a taxa de
variação média é zero nesse intervalo