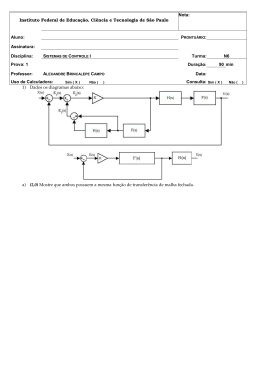
Universidade Federal de Itajubá – Campus
Itabira
Disciplina: BAC 000
Professor: Bruno Zanotelli Felippe
Aluno (a): __________________________ Matrícula: _____ Turma: _____
Lista de Exercícios 11 – Funções Composta e Inversa
1) Determine o domínio da função inversa da função
f ( x) =
2x − 3
.
x+5
1
uma função real definida para x > 0 e seja f-1 (x) a sua inversa. A solução da
x +1
equação f ( x ) = f −1 ( x ) é:
2) Seja f ( x ) =
a)
5− 5
2
b)
5 5
−1
2
c)
5
+1
2
d)
5 −1
2
3) Considerando-se as funções f:R → R, g:R → R e h: R → R, definidas por f(x) = 2x+1, g(x) =
x 2 − x + 2 e h(x) = 3 – x, DETERMINE:
a) f(g(x))
b) g(f(x))
c) g(f(h(x)))
4) A função f de R em R é definida por f(x) =ax +b. Se f(2) = -5 e f(-3) = -10, então f(f(18)) é igual a:
a) –2
b) –1
c) 4
d) 5
5) Sejam as funções reais definidas por f ( x ) = 2 x − 3 e f ( g ( x )) = 10 x − 17 . O valor de x para que
gog ( x ) = 8 será:
a) 2
b) 3
c) 4
d) 5
6) CONSIDERE as funções f ( x ) = 2 x − 1 e g ( x ) = fof ( x ) . O ponto do gráfico de
ordenada 5 é:
a) (2, 5).
b) (17, 5).
c) (9, 5).
g ( x ) que tem
d) (5, 9).
e) (5, 17).
7) Na função f (x) = 3x – 2, sabemos que f (a) = b – 2 e f (b) = 2b + a. O valor de f (f (a) ) é:
a) 2
b) 1
8) Seja f: IR IR a função definida por
c) 0
f (x ) =
2x − 5
3x
. DETERMINE
d) -1
3
f −1   .
2
9) O desenho a seguir é um esboço do gráfico da função f ( x) = 2 + log 0 , 25 ( x + 2) . Determine o valor
de k e a função inversa f
−1
( x) . Construa o gráfico de f
−1
( x) .
y
k
0
x
10) Duas funções são tais que f(x) = x + 3 e f(g(x)) = 5x + 4. Então
GABARITO
1) monitor
2) d
3) a)
2 x 2 − 2 x + 5 b) 4 x 2 + 2 x + 2 c) 4 x 2 26 x + 44
4) c
5) a
6) a
7) b
8) monitor
9) monitor
10) – 3
g( −2)
f (0)
é igual a: