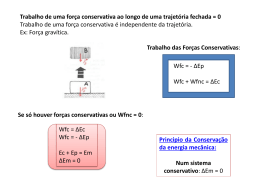
Conservação de energia
Curso de Física I
Nova forma de energia
• Energia potencial (EP)
• Definição
• Que tipo de força leva a EP
– Forças conservativas
– Forças dissipativas
• Forças conservativas e EP
• Exemplos
Energia Potencial
Para descrever os movimentos, baseando-nos em conceitos de
energia, precisamos definir mais um tipo de…
…grandeza escalar associada a um estado de um ou mais corpos.
A energia potencial U é a energia que pode ser associada com a
configuração (ou arranjo) de um sistema de objetos, que exercem
forças uns sobre os outros. Se a configuração muda, a energia
potencial também pode mudar.
Relação entre energia potencial e trabalho:
U  W
Energia potencial: definição
Variação de energia potencial (movimento unidimensional)
x
U  W    F ( x )dx
x0
x0 define uma configuração de referência e x uma configuração geral
Energia potencial para uma dada configuração x:
x
U ( x )  U ( x0 )  U  U ( x0 )   F ( x )dx
x0
Energia potencial: definição (continuação)
Do ponto de vista físico, apenas as variações de energia potencial são
relevantes. Pode-se sempre atribuir o valor zero à configuração de
referência:
U ( x0 )  0
Agora podemos aplicar esse conceito a alguns tipos de força:
•Força elástica
•Força gravitacional
•…em particular perto da superfície terrestre
Força elástica e energia potencial
Configuração de referência: x0 = 0
x
U ( x )  0   (  k ) xdx
Ou:
0
1 2
U ( x )  kx
2
Sistema massa-mola isolado
Sistema isolado: não ocorrem transferências de energia através das
fronteiras do sistema.
Na ausência de atrito : sistema bloco-mola está isolado
1
1 2
2
mv  kx  E  U  K  0
2
2
http://www.ii.metu.edu.tr/emkodtu/met106/lectures/conservation_of_energy/page4.html
Conservação de energia mecânica
em sistemas isolados
Pontos de retorno
v0
Conservação de energia:
 2 E kx2 

v  

m 
 m
Conservação de energia mecânica
2
1 2 1 2
kA
m v  kx  E  E 
2
2
2
Força peso (sistema isolado: bola-Terra)
y
U ( y )  0   (  mg)dy
0
ou
U ( y )  mgy
K  K bola
K    U
K   U  0
Sistema bola – Terra…
1
2
mv  mgy  E mec  cte
2
d
K  0  Emec  Umax  mgd
K max  mgd
vmax  2gd
Pêndulo
U ( y )  mgy
1
2
mv  mgy  E mec  cte
2
h
K  0  Emec  Umax  mgh
Conservação da Energia
Forças Conservativas
F x  U x
1
2
E  mv  U x
2
Forças conservativas e dissipativas
Forças conservativas:
são aquelas para as quais a energia mecânica de um sistema é conservada.
Outra possibilidade de armazenamento de energia em um sistema, além de
potencial e cinética, é a energia interna. Forças conservativas não causam
transformação de energia mecânica em energia interna dentro do sistema.
Exemplo claro de uma força não conservativa: atrito.
Forças não conservativas são chamadas de forças dissipativas.
Lembrem-se da aula passada que o trabalho de uma força de atrito é sempre
negativo!
Watrito  Emec  0
Forças conservativas e dissipativas II
Watrito  Emec
&
Eint erna  Watrito
Generalização da lei de conservação de energia
K  U  Eint  cte
Exemplo:
sem atrito: velocidade máxima do bloco ao passar pela posição de equilíbrio
d
1 2
K  kd
2
2
mvmax
 kd 2
kd 2
v
m
Com atrito: energia cinética diminui e é transformada em calor
K   U  Watr
d
f a  mg
1 2
 kd  mgd
2
 kd 2

v  
 2gd 
 m

Voltando às forças conservativas:
O trabalho feito por uma força conservativa não
depende da trajetória seguida pelos membros
do sistema, mas apenas das configurações
inicial e final do sistema
Exemplo de força conservativa:
força gravitacional no sistema
“homem de pasta” - Terra
O trabalho feito por uma força conservativa,
quando um membro do sistema movimentase por uma trajetória fechada, é igual a zero.
…
L
d
A
B

C
Trabalho realizado pela força peso ao longo do circuito fechado indicado
WA  WB  WC  mgd  mgLsen  0  0
Forças conservativas e energia potencial
xf
W
 F dx  U
x
xi
dU
Fx  
dx
Diagramas de energia e estabilidade do equilíbrio
Diagramas de energia e estabilidade do equilíbrio
Pontos de retorno
Posição de equilíbrio
Diagramas de energia e estabilidade do
equilíbrio
Posição de equilíbrio
Aplicação a ligações químicas:
F>0 repulsão
F
F<0 atração
U
Mínimo de energia
Exemplo de ligação representada por
Um potencial Lenard - Jones
Aplicação a ligações químicas:
Potencial Lenard - Jones
 R
Ur    0
 r

12

R 
  2 0 

 r 
6
F>0 repulsão




F
dU
dr
O mínimo ocorre em
 R
Ur     0
 r

12

R
  2 0

 r
6
 
 
 
F<0 atração
dU
0
dr
 R
Fr   12  0
 r

13

R 
   0 

 r 
Fr  0  rmin  R 0
7




U
Mínimo de energia
Outro exemplo:
Altura h mínima para que o corpo deslizando complete o loop?
No limite N=0
v2
mg  m
r
v 2  gr
Loop…
v2
mg  m
r
2
v  gr
Conservação de energia mecânica:
1
1
2
mgh  mg 2r  mv  mg 2r  mgr
2
2
h  2,5r
Uma lei fundamental
Na presente discussão sobre conservação de energia vimos que essa
lei representa um poderoso atalho para resolver problemas mecânicos.
A conservação de energia é atualmente vista como uma formulação
da dinâmica mais fundamental do que a segunda lei de Newton, mas
são equivalentes nas situações nas quais as leis de Newton são válidas.
Demonstração dessa equivalência: sistemas mecânicos em uma dimensão.
1
E  mv 2  U ( x )  cte
2
dE
0
dt
dE 1 dv2 dU( x ) 1 dv2 dv dU( x ) dx
 m



dt 2
dt
dt
2 dv dt
dx dt
1
dv dU( x )
 dv dU 
 m( 2v ) 
v  v m 
0

2
dt
dx
 dt dx 