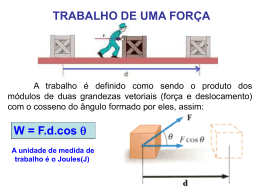
ENERGIA
As leis de Newton permitem analisar vários tipos de movimentos.
Esta análise pode ser bastante complexa, necessitando de detalhes
do movimento que são inacessíveis.
Exemplo: qual é a velocidade final de um carrinho na chegada de um percurso de
montanha russa? Despreze a resistência do ar e o atrito, e resolva o problema usando
as leis de Newton.
vi  0
vf ?
ENERGIA
Até agora abordamos o movimento dum corpo utilizando grandezas como posição,
velocidade, aceleração e força
Resolvemos anteriormente vários problemas de mecânica utilizando esses conceitos
Investigaremos agora uma nova técnica para a análise dos problemas
 inclui definições de algumas grandezas conhecidas mas que na física
essas grandezas tem significados mais específicos do que na vida diária
Começaremos o nosso estudo explorando o conceito de ENERGIA
O termo energia é tão amplo que é difícil pensar numa definição concisa
Devemos nos restringir a determinadas formas de energia, como a manifestada pelo
movimento de um corpo, pela sua posição em relação a outros corpos, pela sua
deformação, etc .
Energia é um conceito que ultrapassa a mecânica de Newton  é relevante também
na mecânica quântica, relatividade , electromagnetismo, etc.
A conservação da energia total de um sistema isolado é uma lei fundamental da
natureza
ENERGIA
Importância do conceito de energia
•
•
•
•
Processos geológicos
Balanço energético no planeta Terra
Reacções químicas
Funções biológicas (máquinas nanoscópicas) 
energia armazenada e energia libertada
• Balanço energético no corpo humano
SISTEMA
Um conceito importante no estudo de energia é o conceito de SISTEMA
 é um modelo de simplificação, em que focalizamos a nossa atenção numa
pequena região do Universo e desprezamos os detalhes sobre o restante do
universo fora do sistema
TRABALHO
Quando empurramos uma caixa ela se desloca  nós realizamos um trabalho sobre a
caixa  a força que exercemos sobre a caixa fez com que ela se movesse

F
d
Trabalho realizado por uma força constante
O TRABALHO realizado por um agente ao exercer
uma força constante sobre um sistema é

F
m


d

x
 
W  F  d  Fd cos
O trabalho é uma grandeza escalar
A unidade de trabalho no SI é o joule (J)
ENERGIA CINÉTICA
A energia cinética K é a energia associada ao estado de movimento de um
corpo
A energia cinética de uma partícula de massa m em movimento com uma
velocidade escalar v é
1
K  m v2
2

v
A energia cinética é uma grandeza escalar
A unidade da energia cinética no SI é o joule (J)
TRABALHO E ENERGIA CINÉTICA

v0
m

F


d
Da segunda lei de Newton

v

x
v  v  2a x d 
2
2
0
1
m (v 2  v02 )  Fx d 
2
Fx  max 
ax 
Fx
m
Fx
v v  2
d 
m
2
2
0
1
1
m v 2  mv02  Fx d
2
2
O lado esquerdo da expressão representa a variação da energia cinética do corpo e o
lado direito é o trabalho realizado pela força sobre o corpo
“Realizar trabalho”, portanto, é transferir energia
TEOREMA DO TRABALHO E DA ENERGIA CINÉTICA
A definição mais geral de trabalho corresponde ao trabalho realizado por uma força
variável
Seja F  F (x) a força resultante que atua sobre uma partícula de massa m
x2
W   F ( x)dx
x1
Integrando entre o estado inicial e o estado final
xf
xf
xf
xf
xf
2
dv
v
W   F ( x)dx   madx  m  adx  m  dx  m  vdv  m
2
xi
xi
xi
xi dt
xi
1
 m(v 2f  vi2 ) 
2
vf
vi
W  K
esse resultado é conhecido como teorema do trabalho e da energia cinética
Quando é feito um trabalho sobre um sistema e a única mudança no sistema é em
sua velocidade escalar, o trabalho feito pela força resultante é igual à variação da
energia cinética do sistema
Exemplo: Trabalho de uma força constante: a força gravitacional na
superfície da Terra
Se o corpo se eleva duma altura d :
 
W  Fg  d  Fg d cos

v  
d

Fg

v0
W  mgd cos  mgd cos 180 0   mgd
o sinal negativo indica que a força gravitacional retira a energia
mgd da energia cinética do objeto durante a subida.

Agora vamos deteminar qual é o trabalho realizado pela força peso sobre
um corpo de 10.2 kg que de cai 1.0 m de altura?

Fg
W  (10 .2 kg) ( 9.8 m/s 2 ) (1.0 m )  100 J
Qual é a velocidade final do corpo, se ele parte do repouso?
K 

vi  0
1
1
1
1
m v 2f  mvi2  m v 2f  0   m v 2f  W
2
2
2
2
vf 
2W

m
2 100 J
 4.4 m/s
10.2 kg
POTÊNCIA
Se uma força externa é aplicada num corpo, e se o trabalho feito por essa força for W
no intervalo de tempo t, então a potência média durante esse intervalo de tempo é
definida como
W
P
t
A potência instantânea P num instante particular é o valor
limite da potência média quando t aproxima-se de zero
Unidade de P no SI:
W dW
P  lim

J/s = watt (W)
t 0
t
dt

dW  dr
 o segundo termo é a velocidade e
P
F
dt
dt


P F v
Unidade de potência HP
criada por Watt para fazer
o marketing de sua
máquina numa sociedade
fortemente dependente do
(e acostumada ao)
trabalho realizado por
cavalos.
1a motivação: retirada da
água das minas de
carvão.
A unidade no sistema inglês é o cavalo-vapor: 1 HP = 760 W
Uma nova unidade de energia pode agora ser definida em termos da unidade de potência:
Um quilowatt-hora é a energia transferida numa hora à taxa constante de 1 kW:
1 kWh  (103 W)(3600s)  3.6 106 J
Exemplo :
100 m RASOS X MARATONA: TRABALHO E POTÊNCIA
Trabalho realizado sobre o corredor de 100 m rasos: 2,1 x 104 J
Trabalho realizado sobre maratonista (42 142 m): 5,9 x 106J
P. A. Willems et al, The Journal of Experimental Biology 198, 379 (1995)
Potência do corredor de 100 m rasos:
Potência do corredor de maratona:
2,110 4 J
P100 
 2100 W
10s
5,910 6 J
Pmar 
 816 W
26060s
ENERGIA POTENCIAL
A energia potencial U é uma forma de energia que pode ser associada com a
configuração (ou arranjo) de um sistema de dois ou mais corpos, que exercem forças
uns sobre os outros.
ENERGIA POTENCIAL GRAVITACIONAL
Consideramos que um estudante levanta um livro de massa m de uma altura inicial
acima do solo, até a uma altura final y 2
y1
O trabalho feito pelo estudante sobre o
sistema livro e Terra é
 


W  F  d  (mg e y )  [( y 2  y1 )e y ]
mgy2
 mgy2  mgy1
O trabalho apresenta uma transferência de
energia para o sistema e que agora aparece na
forma de energia potencial gravitacional
y2
Definimos a grandeza
mgy
como a energia potencial gravitacional U g
mgy1
U g mgy
y1
solo
A unidade da energia potencial
gravitacional no SI é o joule (J)
CONSERVAÇÃO DA ENERGIA MECÂNICA
A introdução da energia potencial nos permite gerar um princípio poderoso e aplicável
universalmente para a resolução de problemas que são difíceis de resolver utilizando as
leis de Newton
Do exemplo anterior  após termos levantado o livro, se agora soltarmos o livro ele
estará sob a influência somente da força gravitacional
Quando o livro cai de y 2 para y 1 , o
trabalho feito pela força gravitacional é
mgy2
Wsobre o livro
 


 Fg  d  (mg e y )  [( y1  y 2 )e y ]
 mgy2  mgy1
y2
Pelo teorema do trabalho e da energia
cinética, o trabalho feito sobre o livro é
Wsobre o livro  K livro 
mgy1
y1
solo
K livro  mgy 2  mgy1
CONSERVAÇÃO DA ENERGIA MECÂNICA
Para o sistema livro-Terra descrito anteriormente, a Terra desloca-se tão lentamente
que praticamente a sua velocidade é nula e a energia cinética do sistema,
é
devido unicamente à energia cinética do livro
K
K livro  K Terra  K  K livro  K
assim
K livro  K  mgy 2  mgy1  (mgy1  mgy 2 )
Agora o nossa energia gravitacional final é
inicial é mgy2  U i
mgy1  U f e a energia gravitacional
Comparando com o sistema livro-Terra  que foi onde definimos a energia potencial
gravitacional
então
(mgy1  mgy2 )  (U f  U i )  U g
K  U g
 escrevemos a equação na forma 
( K f  K i )  (U f  U i )  0

K f  U f  Ki  U i
K  U g  0
ou
(1)
Definimos a soma das energias potencial e cinética como ENERGIA MECÂNICA
Emec  K  U g
Assim a equação (1) é uma formulação da CONSERVAÇÃO DA ENERGIA MECÂNICA
Exemplo : Conservação da energia mecânica
Emec  K  U g
FORÇA ELÁSTICA
Um sistema físico no qual a força varia com a posição  um bloco ligado à uma mola

Faplicada  0
x  x  x0

Fmola

Faplicada  0
Fmola  F ( x)  kx
 Lei de Hook  lei de força para as molas
k é uma constante de força (ou constante elástica)
Fmola 
força restauradora 
o sinal negativo significa que a força exercida pela mola tem sempre direcção oposta
ao deslocamento
ENERGIA POTENCIAL ELÁSTICA
Aplicando
W  U
x
x
x0
0
para o sistema bloco-mola
W   F ( x)dx   F ( x)dx  U  [U ( x)  U (0)]  U ( x)
A configuração de referência é x0= 0 e
Substituindo a força elástica
U (0)  0
F ( x)  kx
x
x
 U ( x)    (kx)dx

0

U ( x) 
1 2
kx
2
na integral
U ( x)  k  xdx 
0
1 2
kx
2
é a energia potencial elástica
A energia mecânica para o sistema bloco-mola
Emec  K  U ( x)  constante
ou
1
1
2
2
Emec  m vbloco  m xmola
 constante
2
2
FORÇA CONSERVATIVA
Forças conservativas  forças para as quais a energia mecânica é conservada
O trabalho feito por uma força conservativa não depende da trajectória, depende
apenas das configurações inicial e final
Exemplos de forças conservativas
• Força gravitacional
• Força elástica
• Força unidimensional que só dependa da posição: F(x)
Conhecendo a energia potencial podemos determinar a força (força conservativa)
  

dW  F  dr  F  dx e x  Fx dx  dU
Fx  

dU
dx
Exemplo: Para um corpo localizado numa distância y acima de algum ponto de
referência, a função energia potencial gravitacional é dada por U g  mgy
Determinamos a força
Fy  
dU g
dy

d
(mgy)  mg
dy
que é a expressão correcta para a força gravitacional
FORÇAS NÃO-CONSERVATIVAS
Forças não-conservativas  O trabalho feito por uma força não-conservativa depende
da trajectória
Exemplos de forças não-conservativas: Força de atrito e Força de arraste
Exemplo 1


Watrito( A  B)   Fatrito  ds   Fatrito LAB 
Watr  A  B  C  f atr  ds   f atr LA B
C
reta
  c mgd

 c mg d / 2 semi-círculo
Nesse caso, não é possível definir uma energia potencial porque o
trabalho da força de atrito depende da trajectória descrita pelo corpo
Exemplo 2:
O bloco de massa m é solto de x = d. Qual é a velocidade do bloco em x = 0?
1 2

K  mv  0 

2
  K  U
1
U  0  kd 2 

2
a) Sem atrito

F
d
1 2 1 2
k
mv  kd  v 
d
2
2
m
x=0
b) Com atrito

F
d
x=0
E  K  U  Watr   c mgd

N

fa


P  mg
1 2 1 2
mv  kd  c mgd
2
2
kd 2
v
 2c gd
m