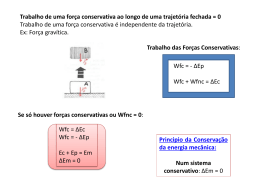
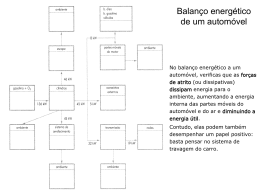
CAPÍTULO 5 – TRABALHO E ENERGIA
AULA 7
DEFINIÇÃO
Define-se trabalho como o produto do valor da força aplicada
sobre um corpo pelo deslocamento que esse corpo sofre na
direcção da força.
r r
r
r
W = F ⋅ ∆r ⇔ W = F ⋅ ∆r ⋅ cosθ ( J )
Em que:
r
F – vector força (N)
r
∆r – vector deslocamento (m)
W = F⋅d (J)
em que:
F – Força (N)
d – deslocamento na direcção da força (m)
1/3
DABP@2008
ENERGIA
Energia Cinética
1
EC = ⋅ m ⋅ v2
2
(J)
Energia Potencial Gravítica
E Pg = m ⋅ g ⋅ h
(J)
Energia Potencial Elástica
E Pe =
1
⋅ k ⋅ x2
2
(J)
FORÇAS CONSERVATIVAS
Uma força é conservativa se o trabalho realizado ao mover
uma partícula entre dois pontos é independente da trajectória.
O trabalho realizado por uma força conservativa, numa partícula que se move numa trajectória fechada, é nulo.
2/3
DABP@2008
FORÇAS NÃO CONSERVATIVAS
Uma força é não conservativa se causa uma alteração da energia mecânica, como por exemplo a força de atrito.
CONSERVAÇÃO DA ENERGIA MECÂNICA
Considerando um sistema isolado, em que as forças internas são
conservativas, temos que:
E M = E C + E P = constante
LEI GERAL DA CONSERVAÇÃO DA ENERGIA
Num sistema isolado, onde há forças interiores conservativas e
não conservativas, a energia mecânica não se conserva, mas
mantém-se constante a totalidade da energia do sistema, isto é, a
soma da energia mecânica com a energia não mecânica interna.
∆E M = ∆E C + ∆E P − f k ⋅ d
3/3
DABP@2008