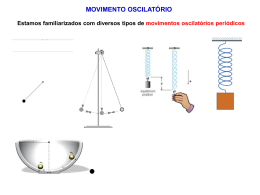
O caso crítico
O caso super crítico
O caso sub-critico
4. (Poli 2006) O Gráfico de x(t), mostrado na figura abaixo, representa a equação
horária de um oscilador criticamente amortecido, para um sistema composto de
um corpo de massa m = 1, 0 Kg preso a uma mola de constante elástica k e
imerso em um líquido viscoso, de coeficiente de resistência viscosa.
(a) Em que instante de tempo a velocidade do corpo será nula, no intervalo
de tempo mostrado no gráfico?
A velocidade é zero quando a
tangente da curva for zero.
Isso corresponde em t = 3 s
(b) A equação horária x(t) pode ser escrita como:
x(t) = e−/2t(a + bt)
Podemos derivar x(t) duas vezes e montar a equação diferencial.
E em seguida mostramos que a identidade vale:
Determine os valores de a e b.
(c) Determine a constante de decaimento e a constante elástica k da mola.
(d) Determine o valor da velocidade inicial do oscilador.
R: (a) t=3s; (b) a = 0, 5 m e b = 0, 5 m/s; (c) = 1 s−1; (d) v = −0.75 m/s.
Oscilações livres com amortecimento viscoso proporcional a velocidade.
f
visc.
z
dx
 b
dt
Mx  bx  kx
b
 
2M
é o atrito viscoso.
t
x(t )  xmaxe cos(1t )
Freqüência angular com dissipação viscosa.
2
 

T
k  b 


M  2M 
2
Item b: Solução da Equação do Movimento com Atrito Viscoso
d 2 x(t )
dx(t )
Mx  bx  kx  M
 b
 kx(t )
2
dt
dt
Vamos testar uma solução com a função:
x(t )  Aet
dx (t )
 A e t
dt
2
d x(t )
2 t

A

e
2
dt
As suas respectivas derivadas são:
Que, substituídas na equação resulta:
2 t
t
t
MA e  bAe  kAe
2
M  b  k  0 a solução para x será:
2
b
k
 b 

 
 
2M
 2M  M
A solução fica na forma:
2
 b

b

 k 

 2 M   2 M   M  t


x(t )  Ae
Observe que temos duas
soluções possíveis!
2
k
 b 
 é muito menor que
então o termo da raiz é complexo!
M
 2M 
Mas! 
e fazendo:
Escrevendo a raiz na forma:
2

k  b  

 i

 t
b

t
 M  2 M  


2M
x(t )  Ae
e
Uma solução parcial será:
x(t )  Ae

b
t
2M
1 
k  b 


M  2M 
 e i1t  e  i1t

2




2
Usando-se a relação de Euler:
A solução final tem a forma:
O termo de atrito viscoso é:
ei1t  e i1t
cos1t 
2
x(t )  xmaxet cos(1t )
b
 
2M
A freqüência angular desta oscilação será:  
1
A oscilação esta em estado crítico quando:
0
k  b 


M  2M 
2
 b 


 2M 
Também chamado caso degenerado:
Uma equação dif. de seg. grau tem 2 soluções
que no caso degenerado já sabemos uma.
x(t )  xmaxe
t
Como será a forma da segunda solução?
A outra solução é procurar a forma :
xI (t )  xII (t )et
e repetindo o
processo anterior de derivação sucessiva.
Concluiremos que a segunda solução :
d 2 xII (t )
 0  xII (t )  A  Bt
2
dt
E assim a solução geral do caso degenerado será:
xI (t )  ( A  Bt)e
t
Item b:
Para t = 0 temos x = 0.5
Para t = 1s temos x = 0
x(t )  ( A  tB)et
x(0)  ( A  0B)e
 0
 0.5  A  0.5
x(1s)  (0.5  (1s) B)e 1s  0  B  0.5
x (t )  (0.5  0.5t )e
t
Item c:
Se v(3) = 0

x (t )   (0.5  0.5(3)) e ( / 2) 3  0.5e ( / 2 )3  0
2
EXTRAIR O VALOR DE GAMA e o k da mola :

2
 0.5    1s
1

2

k
M
A VELOCIDADE SERÁ:
1
x (0)   (0.5  0.5(0)) e (1/ 2) 0  0.5e (1/ 2 ) 0  0.75m / s
2
A equação de d´Alembert
 y ( x, t ) 1  y ( x, t )
 2
0
2
2
x
v
t
2
2
A solução da equação de d´Alembert tem a forma y(x,t) = f(x±vt)
onde o sinal (–) significa que a propagação será progressiva () e
(+) regressiva () e v é a velocidade de propagação da onda.
A busca da sua solução implica em se impor condições de contorno.
A solução y(x,t) = f(x±vt)
pode ser simples ou muito
complexa!
y( x, t )  A cos(kx  t   )
20. (Poli 2006) Uma corda uniforme, de comprimento 20 m e massa 2 Kg, está
esticada sob uma tensão de 10 N.
Faz-se oscilar transversalmente uma extremidade da corda, com amplitude 3 cm e
frequencia de 5 oscilações por segundo. O deslocamento inicial da extremidade é
de 1,5 cm para cima.
(a) Ache a velocidade de propagação v e o comprimento de onda da onda
transversal progressiva que é produzida na corda.
(b) Escreva, como função do tempo, o deslocamento transversal y de um
ponto da corda situado a uma distância x da extremidade que se faz oscilar,
após ser atingido pela onda e antes que ela chegue à outra extremidade.
(c) Calcule a intensidade I da onda progressiva gerada.
Se a massa é 2Kg e o comprimento 20m a densidade linear da corda é :
1
  2 Kg / 20 m  0,1Kgm
A velocidade é dada por:
V 
O comprimento de onda é dado por:
Onde :
f  5s
F


10 N
 10 m / s
0 ,1Kg / m
f  V
1
f  5s   10m / s
1
  2m
 2 y ( x, t ) 1  2 y ( x, t )
 2
0
x 2
V
t 2
Uma solução geral da equação de d´Alembert é:
y ( x, t )  A cos(kx  t   )
2
2
k

 1m 1

2m
  2f  2 5 s 1  10 s 1
A amplitude A é 3cm 0,03m e a fase se obtém impondo y(0,0) = 0,015m(  /3)
2m
3cm
A potência média é :
I  kTA / 2
2
1
  10 s
k  m
T  5 s 1
A  0,015m
18. Determine a amplitude da onda resultante da combinação
de duas ondas senoidais que se propagam no mesmo sentido,
possuem mesma frequência, têm amplitudes de 3, 0 cm e 4, 0
cm e diferença de fase de
R: y(x, t) = 0, 05 sen(kx −
/2 rad
t + 0, 64)
A 1 = 3 sen(kx − t + /2)
A 2 = 4 sen(kx − t)
A 1 = 3 sen(kx − t + /2)
A 2 = 4 sen(kx − t)
25. Duas ondas transversais de mesma frequência = 100 s−1
são produzidas num fio de aço de 1 mm de diâmetro e
densidade 8 g/cm3, submetido a uma
tensão T = 500 N. As ondas são dadas por
y1 = A cos (kx −
t + /6)
y2 = 2Asen(t − kx)
onde A = 2 mm.
(a) Escreva a expressão da onda harmônica progressiva resultante
da superposição dessas duas ondas.
(b) Calcule a intensidade da resultante.
(c) Se fizermos variar a diferença de fase entre as duas ondas, qual é a razão
entre os valores máximo e mínimo possíveis da intensidade da resultante?
R: (a) y = 5, 29 × 10−3 cos(2, 23x − 628t +1, 24).
(b) 9, 8 W.
(c) IMAX IMIN = 9.
y  y1  y 2  A cos(1t  xk1 )  A cos( 2 t  xk 2 )
cos(a )  cos(b)  2 cos[1 / 2( a  b)] cos[1 / 2( a  b)]
k

1
1
y ( x, t )  2 A cos[(
x
t )] cos[ ( k1  k 2 ) x  (1   2 )t )]
2
2
2
2
  (1   2 )  (1   2 )  
k  ( k1  k 2 )  ( k1  k 2 )  k
A( x ,t )



1
1


y ( x, t )  2 A cos[ ( kx  t )] cos[ ( k x   t )]
2
2


Duas oscilações(TONNNNN e TOoNNNNN) com pequena diferença
nas suas freqüências quando somadas, produzem o fenômeno do:
BATIMENTO!!! - TOINHoIINHIINHoIINHoIIII....!
A( x ,t )



1
1


y ( x, t )  2 A cos[ (kx  t )] cos[ (k x   t )]
2
2


TONNN.iiii....
Toonnnnnn.iii.....
TOINHoIIIIINHOIIIIIIINHOIIII...!
24. Uma corda, submetida a uma tensão de 200 N e presa em ambas as extremidades,
oscila no segundo harmônico de uma onda estacionária.
O deslocamento da corda é dado por:
y = (0, 10) sen(x/2) sen(12t) onde x = 0 numa das extremidades da corda, x é dado
em metros e t em segundos.
(a) Qual é o comprimento da corda? y = (0, 10) sen(x/2) sen(12t)
(b) Qual é a velocidade escalar das ondas na corda? y = (0, 10) sen(x/ 2) sen(12 t)
(c) Qual é a massa da corda?
y = (0, 10) sen(x/2) sen(12t)
(d) Se a corda oscilar num padrão de onda referente ao terceiro harmônico,qual será o
período de oscilação?
y = (0, 10) sen(x/2) sen(12t)
R: (a) L = 4 m, (b) v = 24 m/s, (c) μ = 0, 347 kg/m e (d) T = 0, 11 s
y1  A cos(nt  xkn )
y2  A cos(n t  xkn )
y  2 Asen( xkn ) sen(n t )
y  y1  y 2  A cos( n t  xk n )  A cos( n t  xk n )
cos(a)  cos(b)  2 cos[1 / 2(a  b)] cos[1 / 2(a  b)]
y  2 A cos[1 / 2(2 xk n )] cos[1 / 2(2 n t )]
y  2 A cos(xk n ) cos( n t )
y  2 A cos(xk n   / 2) cos( n t   / 2)
y = (0, 10)sen(x/2)sen(12t)
Ondas estacionárias numa corda segundo harmônico.
y  2 Asen( xk2 ) sen(2t )
y = (0, 10) sen(x/2) sen(12t)
Qual o valor de L ?l
2
kn  n
L

2

 L  4m
2
L
y  2 Asen( xk2 ) sen(2t )
y = (0, 10) sen(x/2) sen(12t)
Qual o valor de v ?l
12  2

L
v  v  24m/s
y  2 Asen( xk2 ) sen(2t )
y = (0, 10) sen(x/2) sen(12t)
Qual o valor de m?
y  2 Asen( xk3 ) sen(3t )
y = (0, 10) sen(x/2) sen(12t)
Terceiro harmônico
T3 = ?
2

2

n 
n V 
 3 24m / s  0,11s
Tn
L
T3
4m
Ondas estacionárias numa corda terceiro harmônico.
A velocidade do som e a temperatura do gás(caso gás ideal).
Variação da velocidade do som com a temperatura
A velocidade do som em um gás não é constante, e sim que depende da temperatura.
Da equação de um gás ideal pV=nRT ou então,
 = Cp/Cv
processo ádiabático
A fórmula da velocidade do som é expressa em função da temperatura t do gás em graus
centígrados.
Para obter esta expressão aproximada, tomamos os dois primeiros termos do
desenvolvimento de (1+t/T0)1/2 do binômio de Newton
Sabendo que T0=273.15 K, γ=1.4, R=8.314 J/(K·mol) e M=28.95·10-3 kg/mol, temos que
vs≈331.4+0.61·t
onde 331.4 m/s é a velocidade do som no ar a 0ºC.
Doppler Effect
A Doppler effect is experienced whenever there is
relative motion between a source of waves and an
observer.
When the source and the observer are moving
toward each other, the observer hears a higher
frequency
When the source and the observer are moving
away from each other, the observer hears a
lower frequency
Although the Doppler Effect is commonly experienced
with sound waves, it is a phenomena common to all
waves
Doppler Effect, Moving Observer I
• An observer moves toward a stationary source.
• Due to this movement,
• the observer detects an
• additional number of
wave fronts per unit
time
The frequency heard is
increased
f = v /
Fig 14.8, p. 435
Slide 12
Use positive V0 if the observer is moving toward the source.
Doppler Effect, Moving Observer II
• An observer moves away from a stationary source.
• The observer detects
fewer wave fronts per
second.
• The frequency appears
lower.
Fig 14.9, p. 436
Slide 13
Use negative V0 if the observer is moving away from the source.
Doppler Effect, Source in Motion
•As the source moves toward
the observer (A), the wavelength  appears shorter.
As the source moves away
from the observer (B), the
wave-length  appears longer.
f = v /
Because the frequency is inversely proportional to
the wavelength, f varies in the opposite way as :
Use –vs when the source moves
toward the observer; and +vs
when the source moves away
from the observer
Doppler Effect:
both observer and source moving
Both the source and the observer could be moving
Use positive values of vo and vs if the motion is toward
Frequency appears higher
Use negative values of vo and vs if the motion is away
Frequency appears lower