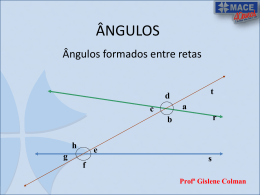
Fotografia de Ana Holck
“Da Série Canteiro de
Obras” 2006
Ângulos formados por duas retas
paralelas e uma transversal
Foto: http://anaholck.com/obras/view/3/30
RECORDANDO...
RECORDANDO...
Duas retas paralelas e uma transversal
Duas retas paralelas e uma transversal
Duas retas paralelas e uma transversal
Duas retas paralelas e uma transversal
Quantos ângulos temos aqui?
Isso mesmo, temos oito ângulos!
Esses ângulos recebem, dois a dois, nomes
especiais
Se estiverem ocupando a mesma posição na reta transversal são
chamados correspondentes.
Esses ângulos recebem, dois a dois, nomes
especiais
Se estiverem ocupando a mesma posição na reta transversal são
chamados correspondentes.
Esses ângulos recebem, dois a dois, nomes
especiais
Se estiverem ocupando a mesma posição na reta transversal são
chamados correspondentes.
Esses ângulos recebem, dois a dois, nomes
especiais
Se estiverem ocupando a mesma posição na reta transversal são
chamados correspondentes.
Esses ângulos recebem, dois a dois, nomes
especiais
Se estiverem do mesmo lado da transversal...
Esses ângulos recebem, dois a dois, nomes
especiais
São chamados ângulos colaterais.
Esses ângulos recebem, dois a dois, nomes
especiais
Se estiverem posicionados em lados alternados da reta transversal
são chamados alternos.
Propriedade fundamental do paralelismo
Duas retas paralelas, cortadas por uma transversal determinam
ângulos correspondentes congruentes.
Exercício
Qual a medida dos ângulos indicados?
Eles estão na mesma posição em relação à reta transversal?
O que podemos afirmar em relação às suas medidas?
Concluímos que x = 40º.
Exercício
Qual a medida dos ângulos indicados?
Eles estão na mesma posição em relação à reta transversal?
O que podemos afirmar em relação às suas medidas?
Assim, precisamos resolver a equação 5x – 40º = 3x + 20º, cujo resultado é x
= 30º.
Ângulos alternos internos
Ângulos alternos internos
Ângulos alternos externos
Ângulos alternos externos
Duas retas paralelas, cortadas por uma transversal determinam
ângulos alternos internos ou externos congruentes.
Exercício
Qual a medida dos ângulos indicados?
Eles estão em que posição em relação à reta transversal?
O que podemos afirmar em relação às suas medidas?
Assim, precisamos resolver a equação 2x + 10º = x + 30º, cujo resultado é x =
20º.
Ângulos colaterais internos
Ângulos colaterais internos
Ângulos colaterais externos
Ângulos colaterais externos
Duas retas paralelas, cortadas por uma transversal determinam
ângulos colaterais internos ou externos suplementares.
Exercício
Qual a medida dos ângulos indicados?
Eles estão em que posição em relação à reta transversal?
O que podemos afirmar em relação às suas medidas?
Assim, precisamos resolver a equação x + 20º = 180º, cujo resultado é
x = 160º.
Exercício
Qual a medida dos ângulos indicados?
Eles estão em que posição em relação à reta transversal?
O que podemos afirmar em relação às suas medidas?
Assim, precisamos resolver a equação 2x + x = 180º, cujo resultado é
x = 60º.
Exercício
Qual a medida dos ângulos indicados?
Os ângulos são concorrentes,
logo são ângulos iguais.
3b - 11° = 2b + 6°
3b - 2b = 6° + 11°
b = 17°
Os ângulos são suplementares, logo a soma entre eles é igual a 180°.
a + (2b + 6°) = 180°
a + 2b + 6° = 180°
a + 2(17°) + 6° = 180°(substituímos b por 17°)
a + 34° + 6° = 180°
a + 40° = 180°
a = 180° - 40°
a = 140°