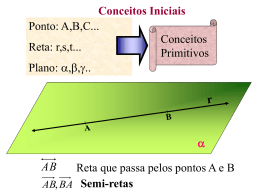
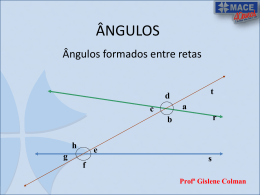
O que é Paralelismo?
Em geometria, Paralelismo é uma
noção que indica se dois objetos (retas ou
planos) estão na mesma direção. Assim,
duas retas são paralelas (símbolo: //) se, e
somente se, são coincidentes( iguais) ou
são coplanares e não têm nenhum ponto
em comum, ou seja, se duas retas
coplanares distintas e uma transversal
determinam ângulos (ou ângulos
correspondentes) congruentes, então
essas duas retas são paralelas
Teorema das retas paralelas
" Se duas retas coplanares e
distintas r e s, e uma transversal
t, determinam um par de ângulos
alternos congruentes, então r é
paralela a s.
Demonstração:
Hipótese: r, s, t pertencem ao plano
A, com r distinta de s, e os ângulos
â = ê, então:
Tese: r // s
Ângulos formados por duas retas paralelas
cortadas por uma transversal
Consideremos as retas r e s traçadas em um mesmo plano,
sem pontos comuns, essas retas são consideradas paralelas; uma
outra reta t, que corta as paralelas considerada transversal ou
secante, que é o nome dado à reta que cruza as retas paralelas.
Essas retas determinam oito Ângulos que possuem
propriedades específicas em congruência e suplemento.
Transversal
Quando a transversal for
perpendicular às duas semiretas paralelas retas todos os
ângulos serão retos (de 90°).
Transversal Perpendicular
às retas
Quando a transversal não
for perpendicular às retas
paralelas,
haverá
quatro
ângulos agudos iguais e
quatro
ângulos
obtusos
iguais.
Transversal nãoperpendicular às retas
Tipos de Ângulos
Posição
Ângulos colaterais internos: estão do mesmo lado da
transversal, entre as paralelas, a soma dos ângulos é 180º.
Ângulos colaterais externos: estão do mesmo lado da
transversal, fora das retas paralelas, a soma dos ângulos é
180º.
Ângulos alternos internos: estão em lados diferentes da
transversal, entre as paralelas e não apresentam o mesmo
vértice, os ângulos são iguais.
Ângulos alternos externos: estão em lados diferentes da
transversal, fora das paralelas e não apresentam o mesmo
vértice.
Ângulos correspondentes: apresentam a mesma medida,
com demarcação estabelecida a um mesmo lado da
transversal.
Ângulos alternos internos: 3 e 6 4 e 5
Ângulos alternos externos: 1 e 8 2 e 7
Ângulos colaterais internos: 3 e 5 4 e 6
Ângulos colaterais externos: 1 e 7 2 e 8
Ângulos correspondentes: 1 e 5 2 e 6 3 e 7
4e8
Teorema de Tales

De acordo com Tales de Mileto,
quando um feixe de retas
paralelas for cortado por duas
ou mais transversais. Todos os
segmentos formados nessas
transversais serão
proporcionais.
Aplicação do Teorema de Tales
O Teorema de Tales pode ser
aplicado em um triângulo que
possui uma reta paralela à
base.para resolver o tales é
necessário meios extremos por
exemplo na ultima figura ficará:
5.20 = 10.10 (100)/(100)=1
resolução desta figura ao lado é
1.
Importância da Geometria
A geometria é de extrema importância no quotidiano das pessoas, pois
desenvolve o raciocínio visual e, sem essa habilidade, elas dificilmente
conseguirão resolver as diferentes situações de vida que forem
geometrizadas; também não poderão se utilizar da Geometria como fator de
compreensão e resolução de questões de outras áreas de conhecimento
humano. A Geometria torna a leitura interpretativa do mundo mais completa,
a comunicação das idéias se ampliam e a visão de Matemática torna-se fácil
de se entender
NESSA PONTE, PODEMOS VER UMA
CONTRIBUIÇÃO DA GEOMETRIA PARA
A SOCIEDADE ATUAL.