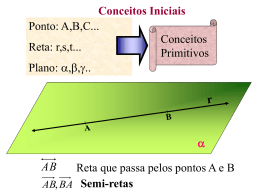
AULA DE REVISÃO
Avaliação Mensal
INTERVALOS
INTERVALOS REAIS

Intervalos reais são subconjuntos dos
números reais determinados por
desigualdades.
Intervalos


Quando o número”não serve”(não
pertence), representamos o intervalo
como aberto (bolinha aberta);
Quando o número “serve” (pertence),
representamos o intervalo como
fechado (bolinha preenchida).
Representação na reta real

Exemplo
-3
-2
-1
0
1
2
3
Simbologia
 menorou igual (bolinha fechada)
 menor(bolinha aberta)
 maior ou igual (bolinha fechada)
 maior (bolinha aberta)
Exercicio: represente na reta
real:
a )x   /  3  x  4
b)x   /  3  x  1
c)x   / x  0
1
5

d ) x   /   x  
3
6

-3
-2
-1
0
1
2
3
4
-3
-2
-1
0
1
2
3
4
-3
-2
-1
0
1
2
3
4
-3
-2
-1
0
1
2
3
4
INEQUAÇÕES



Quando resolvemos inequações
podemos dar sua resposta em duas
formas:
Na reta real
Na notação de conjunto
Exercicio: resolva a inequação
e dê o conjunto solução
a ) x  7  2x  2
x 1 5x  4
b)  
5 3
6
Probabilidade

a)
b)
Num jogo de bingo, as pedras foram
numeradas de 1 a 80. A probabilidade
de sair um número:
Ímpar:
Terminado em 2
ÂNGULOS
COMPLEMENTARES

Quando a soma entre dois ângulos é
de 90 graus, dizemos que esses
ângulos são complementares
ÂNGULOS
SUPLEMENTARES

Quando a soma de dois ângulos for
de180 graus, dizemos que esses
ângulos são suplementares.