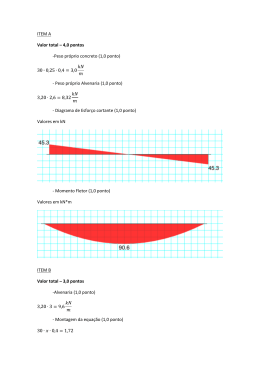
INTERAÇÃO ENTRE AS PARTES DE
UM CORPO
Problema real
Modelo
Informações das ações transitam ao longo do corpo!
De que forma isto acontece?
y
Imagina-se que o corpo em
equilíbrio, referenciado em relação
a um sistema global de
coordenadas (xyz), seja recortado
virtualmente através de um plano.
x
z

q

q
q   F / L2

FR

MR

 MR

 FR
Idealiza-se que a interação entre
as partes do corpo seja
representada por uma distribuição
de forças ao longo de toda a
superfície virtual de corte.
Abstraindo-se da forma da
distribuição de forças ao longo da
superfície virtual de corte, a
atenção será voltada às
resultantes (sistema equivalente)
em relação a um ponto localizado
no centróide desta superfície.
Referenciam-se todas as forças e momentos em relação ao sistema global. Portanto, pelo
princípio da ação e reação, as entidades atuantes nas superfícies internas virtuais são
representadas com os mesmos módulo e direção, porém com sentido contrário (sinal negativo).
Com o objetivo de isolar os efeitos que estas resultantes submetem o corpo, estas são
decompostas numa direção perpendicular à superfície virtual de corte e numa outra
sobre o plano de corte. Nesta decomposição, assume-se um novo sistema de
coordenadas, dito local, que acompanha o plano de corte e que apresenta convenções
contrárias nas superfícies opostas. Desta forma, elimina-se o sinal negativo consistente
com o princípio da ação e reação quando a referência é o sistema global.
Q

FR
N
N

 FR
Q
N: Esforço normal. Tende a afastar (tração - positivo) ou aproximar (compressão negativo) as partes do corpo na direção perpendicular à superfície de corte.
Q: Esforço cortante. Tende a deslizar relativamente as partes do corpo numa direção
paralela à superfície virtual de corte.

 MR
M
T
T
M

MR
T: Momento torçor. Tende girar relativamente as partes do corpo em torno da direção
perpendicular à superfície virtual de corte.
M: Momento fletor. Tende girar relativamente as partes do corpo em torno de um eixo
paralelo à superfície virtual de corte.
Interação entre as Partes numa Barra Reta
– Esforços Normal e Cortante –
A (área da seção transversal)
y
N (esforço normal)
x
z
centróide
px 
b (base da seção transversal)
N
A
Distribuição
constante ao
longo de toda a
seção de corte
y
x
z
Q (esforço cortante)
h (altura da seção transversal)
Distribuição
quadrática ao
longo da altura
da seção
transversal
6Q  2 h 2 
p y  3  y  
bh 
4
Interação entre as Partes numa Barra Reta
– Momentos Fletor e Torçor –
Seção transversal simétrica
em relação ao eixo y
y
M (momento fletor)
x
z
Eixo neutro:
interação nula
centróide
px  
Distribuição
linear ao longo
da altura da
seção de corte
y
z
My
I zz
T (momento torçor)
x
p 
J (momento polar de inércia)
Tr
J
Distribuição
circunferencial
linear ao longo
do raio da seção
transversal