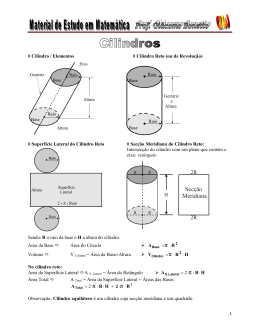
CORPOS REDONDOS
CILINDROS
Cilindro
Considere dois planos paralelos,  e σ,
um círculo C de raio r contido em , e
uma reta s que intercepta planos  e σ.
Chama-se cilindro circular, ou apenas cilindro, a figura geométrica
formada pela reunião de todos os segmentos de reta paralelos à reta
s, com uma extremidade em um ponto de C e a outra em um ponto do
plano σ.
Elementos do cilindro
Classificação dos cilindros
Podemos classificar os cilindros de acordo com a inclinação da reta s
em relação aos planos  e σ que contêm as bases:
se a reta s é perpendicular
se a reta s não é perpendicular
aos planos  e σ, o cilindro
aos planos  e σ, o cilindro é
é reto (g = h).
oblíquo (g ≠ h).
Observações
 Um
cilindro
circular
reto
também
é
denominado cilindro de revolução, pois pode
ser obtido pela rotação de uma superfície
retangular em torno da reta que contém um
dos lados dessa superfície. A medida desse
lado é igual à altura h do cilindro, e a
medida do lado perpendicular a esse é igual
à medida do raio r da base do cilindro.
Observações
 Se um cilindro reto tem altura igual ao dobro da medida do raio da
base (h = 2r), ele é chamado cilindro equilátero.
Secção meridiana de um cilindro
Uma secção meridiana de um cilindro é determinada pela intersecção
do cilindro com um plano que contenha seu eixo.
Secção transversal de um cilindro
Uma secção transversal de um cilindro é a intersecção do cilindro com
um plano paralelo ao plano da base.
Planificação da superfície de um cilindro reto
Área da superfície e volume de um cilindro reto
Abase = r2
Alateral = 2rh
Atotal = 2r(r + h)
Vcilindro = r2h
Exercícios
1.
Dado um retângulo de dimensões 3 cm e 5 cm, comparar a área
lateral e a área total da superfície dos cilindros de revolução dele
obtidos.
Resolução
Fazendo a rotação do retângulo em torno do lado que mede 3 cm,
obtemos um cilindro reto de raio 5 cm e altura 3 cm. Então:
Alateral = 2 ∙  ∙ 5 ∙ 3 = 30
Atotal = 2 ∙ 5 ∙  ∙ (5 + 3) = 80
Logo, esse cilindro tem área lateral de 30 cm2 e área total de 80 cm2.
Resolução
O outro cilindro de revolução tem raio 3 cm e altura 5 cm. Então:
Alateral = 2 ∙  ∙ 5 ∙ 3 = 30
Atotal = 2 ∙ 3 ∙  ∙ (3 + 5) = 48
Logo, esse cilindro tem 30 cm2
de área lateral e área total de 48 cm2.
Portanto, as áreas laterais dos cilindros obtidos são iguais.
No entanto, quando fazemos a rotação do retângulo em torno do lado menor,
a área total da superfície do cilindro é maior.
2.
Calcular a razão entre a área da base e a área da secção meridiana
de um cilindro equilátero.
Resolução
Vamos considerar um cilindro equilátero de
altura h e cuja base é um círculo de raio r.
A área da base é: Abase =  ∙ r2
Como um cilindro equilátero tem a altura igual ao dobro do raio (h = 2r), a
secção meridiana é um quadrado de lado 2r.
A área da secção meridiana é: Asecção meridiana = 2r ∙ 2r = 4r2
 ∙ r2= _

Assim, temos: ____
4 ∙ r2
4
3.
Considerar três cilindros circulares retos: C, de altura h e base de
raio r; cilindro C’, de altura h e base de raio 2r; e cilindro C’’, de
altura 2h e base de raio r.
a) Comparar o volume de C’ com o de C.
b) Comparar o volume de C’’ com o de C.
c) Comparar o volume de C’ com o de C’’.
Resolução
Primeiro calculamos o volume de C: V = r2h
a) C’ tem volume V’ =  ∙ (2r)2 ∙ h = 4(r2h), ou seja: V’ = 4V
Portanto, o volume de C’ é o quádruplo do volume de C.
b) C’’ tem volume V’’ =  ∙ r2 ∙ (2h) = 2(r2h), ou seja: V’’ = 2V
Portanto, o volume de C’’ é o dobro do volume de C.
c) Dos itens anteriores, temos: V’ = 4r2h = 2(2r2h), ou seja:
V’ = 2V’’
Portanto, o volume de C’ é o dobro do volume de C’’.
4. Quantos centímetros quadrados de material são usados,
aproximadamente, para fabricar a lata de óleo indicada ao lado e o
seu volume?
Solução
Al = 2 rh  2 . 3,14 . 4 .19  477 , 28 cm 2
Ab =  r 2  3,14 . 4 2  50 , 24 cm 2
AT = 2 Ab + Al
Óleo
AT = 477 , 28 + 100 , 48  577 , 76 cm 2
V = Ab . h
8 cm
V = 50, 24.19
V = 954,56 cm3
19 cm
De acordo com o problema, o volume desse cilindro deverá ser de
1 litro ou 1 dm3. Sabemos que o raio da base será de 5 cm, que
equivale a 0,5 dm. Utilizando a fórmula do volume, teremos:
Portanto, a lata deverá ter uma altura
de, aproximadamente, 13 cm.