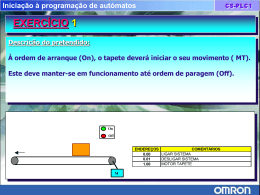
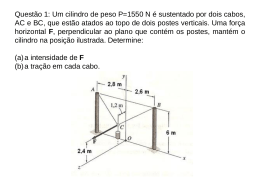
Cilindro
Segmento: Ensino Médio
Disciplina: Matemática
Tema: Sólidos Geométricos - Cilindros
Cilindro
Base
eixo
*O
b
R
g
g h
*O
a
Base
a
90º
R é raio da base
h é altura
g é geratriz
A Fig. mostra um
Cilindro Oblíquo.
Cilindro
Cilindro Circular Reto
ou Cilindro de Revolução
A
* O’
B
g
h
g
C
R
R
*O
D
1) o eixo é perpendicular
aos planos das bases.
2) g = h
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
A
B
D
C
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Cilindro de Revolução:
Um Cilindro reto pode ser obtido ao girar um
retângulo em torno de um dos seus lados.
A
B
D
C
Cilindro
Seção Meridiana
Retângulo ABCD é a seção meridiana do cilindro.
Seção
Meridiana
A
h
* O’
B
C
*
O
2R
D
Se ABCD
é um
quadrado 
cilindro
eqüilátero
Cilindro eqüilátero é o cilindro reto em que
h = 2R
Cilindro
Seção Transversal
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
h
x
R
Cilindro
Planificação :
R
h
x
R
2pR
R
Cilindro
Áreas e Volumes
Área Base
( Ab )
Ab = p R2
Área Lateral AL = 2p Rh
( AL )
Área Total
( At )
Volume
( V)
At = AL+ 2 Ab
V = p R 2. h
Cilindro
Ex.1:
A base de um cilindro de revolução é equivalente a secção meridiana. Se o raio da base é
unitário, então a altura do cilindro é:
a) p
b) 1
2
c)
p
d) p
2
e)
p
2
(FUVEST-SP)
Cilindro
Ex.2:
Dois cilindros, um de altura 4 e outro de altura 6, tem para perímetro de suas bases 6 e 4,
respectivamente. Se V1 é volume do primeiro
e V2 o volume do segundo, então:
a) V1 = V2
b) V1 = 2V2
c) V1 = 3V2
d) 2V1 = 3V2
e) 2V1 = V2
(PUC - RS)
Cilindro
Ex.3:
Um cilindro eqüilátero está inscrito em um
cubo de volume 27 cm3. Qual o volume do
cilindro?
a) 9p cm3
4
c) 27p cm3
4
b) 27p cm3
8
d) 27p cm3
e) 54p cm3
(UF-PA)
Cilindro
(CEFET-PR) O volume do cilindro eqüilátero, cujo
comprimento do círculo da base é C, é:
A)
B)
C)
D)
Como V = pR2.h
E o “cilindro eqüilátero” possui h = 2R
Então, V = pR2.2R
V = 2pR3
“comprimento do círculo da base é C”, implica dizer que
2pR = C
Daí, R = C/2p
V = 2p(C/2p)3
V = _2pC3
8p3
V = __C3_
4p2
Cilindro
(UFRN-RN) Se um cilindro eqüilátero mede 12 m
de altura, então o seu volume em m3 vale:
A) 144p
B) 200p
C) 432p
D) 480p
“cilindro eqüilátero” possui h = 2R
12 = 2R
_12_ = R = 6
2
Como V = pR2.h
V = p62.12
12 m
V = p36.12
V = 432p