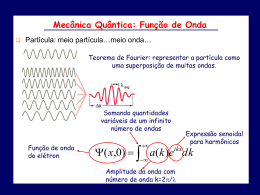
Introdução à Nanotecnologia
Introdução à Mecânica Quântica
Dualidade onda-partícula
“Não leve essa aula muito a sério… apenas relaxe e
desfrute dela. Vou contar para vocês como a natureza
se comporta. Se você admitir simplesmente que ela
tem esse comportamento, você a considerará
encantadora e cativante. Não fique dizendo para si
próprio: “Mas como ela pode ser assim?” porque
nesse caso você entrará em um beco sem saída do
qual ninguém escapou ainda. Ninguém sabe como a
natureza pode ser assim”.
Richard Feynman (1918-1988)
Prêmio Nobel de Física 1965
1.1 - A mecânica dos objetos microscópicos
Mecânica clássica - Mecânica dos objetos macroscópicos: Leis de
Newton. Partículas ou corpúsculos. Física corriqueira, intuitiva.
Física das ondas: Ondas sonoras, eletromagnéticas. Difração e
interferência.
Mecânica quântica: Mecânica dos objetos microscópicos (átomos e
elétrons, por exemplo). Se comportam em muitas situações como
partículas e em outras como ondas.
Mecânica quântica: teoria abstrata ou aplicada?
Invenções que só foram possíveis por causa da mecânica quântica:
computador, laser, energia nuclear, imagens de ressonância magnética, etc.
Em 2000, a revista Scientific American estimou que 1/3 do produto interno
bruto dos EUA estava ligado à mecânica quântica!
1.2 - A experiência de fenda dupla com projéteis
http://www.physik.uni-muenchen.de/didaktik/Computer/Doppelspalt/dslit.html
• Descrição
• Simulação
• Projéteis chegam em pacotes idênticos
• Projéteis não apresentam interferência
P12  P1  P2
P1
P12
P2
http://www.upscale.utoronto.ca/GeneralInterest/Harrison/DoubleSlit/DoubleSlit.html
1.3 - A experiência de fenda dupla com ondas
Detetor
móvel
I1
I12
Fonte
I2
Anteparo
x
x
• Ondas podem ter qualquer intensidade: contínua, não discreta.
• Ondas mostram interferência:
I12  I1  I 2
d1  d 2  n
I12  I1  I 2  2 I1I 2 cos
Casos especiais:
Interferência construtiva (=0):
d1  d 2  n
d1  d 2  2n  1
1
2
Interferência destrutiva (=):

2
x
d1
d2
1.3 - A experiência de fenda dupla com elétrons
Supondo que o impacto de um elétron no detetor produza um som de
“clique”:
(a) Todos os “cliques” são idênticos.
(b) Os “cliques” acontecem de forma bastante errática. O instante de
chegada dos elétrons parece ser imprevisível.
(c) Nunca escutamos dois “cliques” simultaneamente, ou seja, os elétrons
chegam um de cada vez.
Elétrons chegam em pacotes
idênticos: são como “bolinhas”!
• Podemos medir a probabilidade ou taxa média de chegada
do elétron em uma certa posição x.
• Simulação
Elétrons apresentam interferência!!!
Detetor
móvel
P1
P12
Fonte
de
elétrons
P2
Para elétrons:
P12  P1  P2
Anteparo
x
x
Decididamente, elétrons NÃO
são como “bolinhas”…
Resumo
• Projéteis chegam em pacotes idênticos e não apresentam
interferência:
P12  P1  P2
• Ondas podem ter qualquer intensidade e apresentam
interferência:
I12  I1  I 2
• Elétrons chegam em pacotes idênticos e apresentam
interferência!
P12  P1  P2
Dualidade onda-partícula: Elétrons às vezes se
comportam como ondas, outras vezes como partículas
1.4 - A luz como partícula: O Efeito Fotoelétrico
Hertz
(1886)
Lenard
Millikan
(1914)
Nobel 1923
Corrente vs. voltagem para luz de mesma
frequência mas intensidades diferentes
Elétrons são emitidos com
energia cinética máxima:
Tmax  eV0
Potencial de retardo ou potencial de corte
V0 em função da frequência da luz 
V0
Problemas com a teoria clássica:
1. Intensidade: Energia
máxima dos elétrons emitidos
deveria depender da
intensidade da onda
eletromagnética.
Frequência 0
de corte

Tmax = 0 , elétrons não são mais
arrancados do eletrodo
2. Frequência: Efeito
fotoelétrico deveria ocorrer
para qualquer frequência.
3. Tempo de atraso: Para luz
suficientemente fraca, o
elétron só poderia ser emitido
quando acumulasse energia
suficiente da onda, que
deveria ser absorvida de
forma contínua. Nenhum
tempo de atraso jamais foi
detectado.
A hipótese do fóton - Albert Einstein,
1905 (Nobel 1921)
• Energia da luz é quantizada em “pacotes” (fótons) de valor
E = h, onde h = 6,63×10-34 J.s é a constante de Planck
• O fóton carrega também momento linear:
E h h
p 

c
c

W
W
• Energia é transferida de forma
discreta, através de processos
individuais de colisões entre 1
fóton e 1 elétron
W : função trabalho
(propriedade do material)
• Fótons com energia h < W não vão conseguir arrancar
elétrons do metal: h 0= W
Tmax  eV0  h  W 
V0
 h(  0 ) 
h(  0 )
V0 
e
0

Inclinação da reta fornece
a constante de Planck!
Millikan obteve h = 6,57×10-34 J.s
Aplicação: célula fotoelétrica
1.4 – Ondas de matéria
Como obter P12? Use a matemática das ondas!
Associar uma onda ao elétron: Louis de Broglie
(Tese de Doutorado, 1924; Nobel 1929)
Mesmas relações sugeridas por Einstein para
fótons:
E  h
p
h

p2
Exemplo: elétron com energia T  2m  p  2m T ;
cinética de 100 eV, qual o
h
h
comprimento de onda?
 
 0,12 nm
p
2m T
Verificação experimental: difração de elétrons por cristais
(Davisson-Germer e Thomson, 1927; Nobel 1937)
Microscopia eletrônica de
transmissão de alta resolução
Davisson
Thomson
“J. J. Thomson (pai) mostrou
que o elétron é uma partícula,
G. P. Thomson (filho) mostrou
que o elétron é uma onda”
Nanopartícula de CdSe
Por que as propriedades ondulatórias da matéria
não são notadas no dia-a-dia?
Problema: qual o comprimento de onda de um objeto de 1 kg
movendo-se a 10 m/s?
h
h 6,631034 J.s
 

 6,631035 m
p mv
10 kg.m/s
Os Postulados da Mecânica Quântica
2.1 – A Função de Onda
Uma partícula quântica é descrita por uma função de onda (r,t), que:
• Contém toda a informação sobre a dinâmica da partícula
• É uma função complexa
• É unívoca, finita e contínua
• Tem derivadas unívocas, finitas e contínuas
(Na maior parte dos exemplos, vamos nos restringir a uma
dimensão, por simplicidade)
Exemplo: partícula livre (não sofre a ação de forças).
• Momento linear é constante.
• Função de onda deve reproduzir os postulados de de Broglie:
  h p ; E  h
 ( x, t )  Aei ( kxt ) (onda plana)
k
2
(vetorde onda)

  2 (frequencia angular)
h
h
p
k  k ; E 
  
2
2
Interpretação probabilística da função de onda
Max Born 1926 (Nobel 1954)
Se, no instante t, é feita uma medida da localização da partícula
associada à função de onda (x,t), então a probabilidade P (x,t)dx de
que a partícula seja encontrada entre x e x+dx é igual a *(x,t) (x,t)dx.
Densidade de probabilidade : P ( x, t )   * ( x, t ) ( x, t )

Normalizacao :   * ( x, t ) ( x, t )  1
-
Note que P (x,t) é real e não-negativa, como toda probabilidade…
“Deus não joga
dados com o
universo”
“Einstein, pare
de dizer a Deus
o que fazer”
(Albert Einstein)
(Niels Bohr)
2.2 – A Equação de Schroedinger
(Schroedinger 1926, Nobel 1933)
   ( x, t )
 ( x, t )


V
(
x
,
t
)

(
x
,
t
)

i

2
2m x
t
2
2
V(x,t): energia potencial
Em 3D :





 (r , t )
2

  (r , t )  V (r , t ) (r , t )  i
;
2m
t
2
2
2



Laplaciano:  2  2  2  2
x
y
z
2
Exemplo: partícula livre (V=0)
 2  2  ( x, t )
 ( x, t )

 i
2
2m x
t
Separacaode variaveis:  ( x, t )   ( x) (t )
  [ ( x) (t )]
[ ( x) (t )]

 i
2
2m
x
t
1   2 d 2  1  d 
 i   E

2 
  2m dx    dt 
2
2
Relação de
dispersão  (k)

  ck
(fotons)
d
d
iE
i
 E 
     (t )  e iEt   e it ( E   )
dt
dt

 2 d 2
d 2
2m E


E





2
2
2
2m dx
dx

d 2
 2k 2
 ikx
2
Solucao : ( x)  e  2   k   E 
dx
2m
Solucao geral :  ( x, t )  Aei ( kxt )  Bei ( kxt )
k 2

2m
(elet rons)
k
2.3 – Operadores Quânticos
A cada grandeza física corresponde um operador
matemático, que opera na função de onda.
Operadormomentolinear pop :

pop  i
x
O que acontecequando operamospop na funcaode onda da particulalivre?


 i ( kxt )
pop  ( x, t )  i
e
 k ei ( kxt )  k ( x, t )  p ( x, t )
x
Quando aplicamos um operador a  e obtemos de volta a própria 
multiplicada por uma constante, diz-se que  é uma autofunção do
operador, com autovalor igual à constante obtida. Quando isso acontece,
diz-se que a grandeza física associada tem valor bem definido, com
incerteza nula.
Assim, a  da partícula livre é uma autofunção do operador momento,
com autovalor ħk.
Operadorenergia Eop :

Eop  i
t
O que acontecequando operamosEop na funcaode onda da particulalivre?


 i ( kxt )
Eop  ( x, t )  i e
  ei ( kxt )   ( x, t )  E ( x, t )
t
A  da partícula livre também é uma autofunção do
operador energia, com autovalor ħ.
Operadorenergia cineticaTop :
 
 

 i   i 
pop pop 
2 2
x 
x 
Top 


2m
2m
2m x 2
Operadorposicao xop  x
Noteque a  da particulalivre nao e' uma autofuncaoda posicao:
x  xei ( kxt )  C
Note que a equação de Schroedinger pode ser escrita em
termos dos operadores:
 2  2  ( x, t )
 ( x, t )

 V ( x , t )  ( x , t )  i
2
2m x
t
Top  Vop   Eop 
Top  Vop  H (operadorHamiltoniano)
H  Eop 
2.4 – Valores Esperados
• Em geral, o resultado de uma medida de uma certa
grandeza física tem uma natureza aleatória: não pode ser
previsto com total certeza.
• Pergunta: qual o valor esperado ou valor mais provável
(do ponto-de-vista estatístico) do resultado de uma medida?
Seja uma certagrandeza fisica Q associada ao operadorQop .
O valoresperado Q da medida no instantet e' dado por :

Q    * ( x, t )Qop  ( x, t ) dx

2.5 – A Equação de Schroedinger independente do
tempo Considerea equacao de Schroedinger quando
o potencialnao depende do tempo: V ( x, t )  V ( x)
 2  2  ( x, t )
 ( x, t )

 V ( x )  ( x , t )  i
2
2m x
t
Novamente,separacaode variaveis:  ( x, t )   ( x) (t )
 2  2 [ ( x) (t )]
[ ( x) (t )]

 V ( x) ( x) (t )  i
2
2m
x
t
1   2 d 2 
1  d 
 V ( x)  i   E

2 
  2m dx 
  dt 
d
d
iE
i
 E 
     (t )  e iEt   e it ( E   )
dt
dt

 2 d 2

 V ( x)  E
2
2m dx
 Equacao de Schroedinger independent e do tempo
Define- se o operadorHamiltoniano :
2 d 2
H  Top  Vop  
 V ( x)
2
2m dx
H  E  Equacao de autovalores
Sua solucao permiteencontraros autovalores
da energia
Exemplos de aplicação da Equação da
Schroedinger em 1D
3.1 – Partícula livre (revisão)
E
Potencial V ( x)  0
 2 d 2
Eq. Schroedinger : 
 E
2
2m dx
Solucoes : ( x)  Aeikx  Beikx
 2k 2
Energias: E 
2m
 2k 2
E
2m
k
Qualquer energia positiva
é permitida (energia varia
de forma contínua)
3.2 – Poço de potencial infinito
V


Potencial:
Região
proibida
Região
proibida
0, 0  x  L
V ( x)  
, x  L ou x  0
0
L
x
Em x  L ou x  0 (regiao proibida):
 ( x)  0
Em 0  x  L, temos V ( x)  0 :
 2 d 2
Eq. Schroedinger : 
 E (comoa particulalivre)
2
2m dx
2 2

k
Solucao :  ( x)  Aeikx  Beikx ; E 
2m
Funcao de onda deve ser continuaem x  0 e x  L
CONDICAO DE CONT ORNO:
 ( 0)   ( L )  0 
Em x  0 :  (0)  A  B  0  A   B
 ( x)  Aeikx  e ikx   Asen kx (a menosde uma constante...)
Em x  L :  ( L)  Asen kL  0  kL  n (n  1,2,3...)
 2 k n2  2  2 n 2
n
kn 
 En 

(energiaquantizada)
2
L
2m
2m L
Funcoesde onda :  n ( x)  Ansen k n x
n : número quântico
V
 (x)
L
0
0
n=2
L
n=3
L
0
L
n=4
Região
proibida
n=1

E3
Região
proibida
0

E2
E1
0
L
x
Comentários de validade
geral:
•Partículas que estão confinadas
a uma região do espaço têm um
espectro discreto de energias, ou
seja, têm energias quantizadas
• Matematicamente, isto decorre
das condições de contorno
impostas nas extremidades (como
numa corda vibrante)
• Quanto maior o número de
zeros (nós) da função de onda,
maior a energia do estado
Exemplo em
nanotecnologia: Poços
quânticos semicondutores
3.3 – Potencial degrau, barreira de potencial e
efeito túnel
Efeito túnel: Atravessando barreiras
P = 100 %
P < 100 %
Barreira
100% - P
Potencial degrau
V
V0
E < V0
E
1
2
0
x
Regiao 1 - eletronlivre:
Regiao 2 - Eq. Schroedinger :
 1 ( x)  Aeikx  Beikx (incidente refletida)
 2 d 2

 V0  E 
2
2m dx
d 2 2mV0  E 

 , V0  E   0
2
2
dx

Solucao : 2 ( x)  Cex  Dex ,
 2k 2
2m E
E
k 
2m

2mV0  E 
onde  

Encontrar B, C e D em termos de A
 1 ( x)  Aeikx  Beikx , x  0
Deve ter derivadascontinuasem x  0 :
 2 ( x)  Cex  Dex , x  0
d 1
dx
Funcao de onda nao pode divergir :
x 0
d 2

dx

x 0
ikA  ikB  D (2)
C 0
Deveser continuaem x  0 :
A  B  D (1)
Combinando(1) e (2),obtemos:
ik  
ik ( A  B )   ( A  B )  B 
A
ik  
ik  
2ik
A
A D D
A
ik  
ik  
Barreira de potencial e Efeito Túnel
 (x)
V
V0
e  x
x
0
incidente
 (x)
refletido
V
transmitido
0
Existe uma probabilidade
de encontrar o elétron na
região classicamente
proibida
a
x
Simulações:
http://www.neti.no/java/sgi_java/WaveSim.html
Se a barreira for
suficientemente pequena
(largura a) o elétron
poderá ser transmitido
(tunelar) com uma certa
probabilidade: EFEITO
TÚNEL
Ptrans   2 (a )  e  2a
2
“Efeito túnel” em ondas clássicas:
Ondas evanescentes
Reflexão interna total
http://wwwhome.math.utwente.nl/~hammerm/Metric/Illust/parcoreM.html
Acoplamento entre
guias de onda
Aplicação em nanotecnologia: STM
(scanning tunneling microscope)
Visualização e manipulação de átomos
Heinrich Rohrer (à esquerda) e Gerd K. Binnig (direita), cientistas do
IBM's Zurich Research Laboratory, na Suíça, receberam
o Prêmio Nobel de Física de 1986 por seu trabalho
no desenvolvimento do microscópio de varredura por tunelamento.
STM
Visualizando átomos
Superfície de Níquel
(IBM Research Labs, California)
Superfície de Silício
(Naval Research Lab,
Wash DC, USA)
Referências:
• “Materiais e Dispositivos Eletrônicos”, Sergio M. Rezende,
Editora Livraria da Física – Seções 2.3, 2.4, 3.1, 3.2, 3.3 e
3.4.
• “Física Quântica”, Eisberg e Resnick, Editora Campus Seções 2.2, 2.3, 2.5, 2.4, Cap. 3, 5.1 a 5.5, 6.1, 6.2, 6.3, 6.5,
6.8 e 6.9
• “Lectures on Physics”, Feynman, Vol. 1, Cap. 37
(interferência com fenda dupla)
Problemas:
Rezende 2.8, 2.9, 2.12, 2.13, 3.2, 3.6, 3.7. 3.9, 3.10
Reproduza os cálculos realizados nesta aula.
Apresentação de Rodrigo Capaz