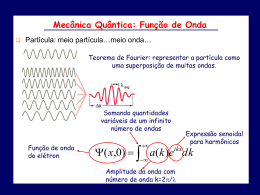
Os Postulados da Mecânica Quântica
2.1 – A Função de Onda
Uma partícula quântica é descrita por uma função de onda (r,t), que:
• Contém toda a informação sobre a dinâmica da partícula
• É uma função complexa
• É unívoca, finita e contínua
• Tem derivadas unívocas, finitas e contínuas
Interpretação probabilística da função de onda
Max Born 1926 (Nobel 1954)
Se, no instante t, é feita uma medida da localização da partícula
associada à função de onda (x,t), então a probabilidade P (x,t)dx de
que a partícula seja encontrada entre x e x+dx é igual a *(x,t) (x,t)dx.
Densidade de probabilidade : P ( x, t )   * ( x, t ) ( x, t )

Normalizacao :   * ( x, t ) ( x, t )  1
-
Note que P (x,t) é real e não-negativa, como toda probabilidade…
“Deus não joga
dados com o
universo”
“Einstein, pare
de dizer a Deus
o que fazer”
(Albert Einstein)
(Niels Bohr)
2.2 – A Equação de Schroedinger
(Schroedinger 1926, Nobel 1933)
   ( x, t )
 ( x, t )


V
(
x
,
t
)

(
x
,
t
)

i

2
2m x
t
2
2
V(x,t): energia potencial
Em 3D :





 (r , t )
2

  (r , t )  V (r , t ) (r , t )  i
;
2m
t
2
2
2



Laplaciano:  2  2  2  2
x
y
z
2
Exemplo: partícula livre (V=0)
 2  2  ( x, t )
 ( x, t )

 i
2
2m x
t
Separacaode variaveis:  ( x, t )   ( x) (t )
  [ ( x) (t )]
[ ( x) (t )]

 i
2
2m
x
t
1   2 d 2  1  d 
 i   E

2 
  2m dx    dt 
2
2
Relação de
dispersão  (k)

  ck
(fotons)
d
d
iE
i
 E 
     (t )  e iEt   e it ( E   )
dt
dt

 2 d 2
d 2
2m E


E





2
2
2
2m dx
dx

d 2
 2k 2
 ikx
2
Solucao : ( x)  e  2   k   E 
dx
2m
Solucao geral :  ( x, t )  Aei ( kxt )  Bei ( kxt )
k 2

2m
(elet rons)
k
2.3 – Operadores Quânticos
A cada grandeza física corresponde um operador
matemático, que opera na função de onda.
Operadormomentolinear pop :

pop  i
x
O que acontecequando operamospop na funcaode onda da particulalivre?


 i ( kxt )
pop  ( x, t )  i
e
 k ei ( kxt )  k ( x, t )  p ( x, t )
x
Quando aplicamos um operador a  e obtemos de volta a própria 
multiplicada por uma constante, diz-se que  é uma autofunção do
operador, com autovalor igual à constante obtida. Quando isso acontece,
diz-se que a grandeza física associada tem valor bem definido, com
incerteza nula.
Assim, a  da partícula livre é uma autofunção do operador momento,
com autovalor ħk.
Operadorenergia Eop :

Eop  i
t
O que acontecequando operamosEop na funcaode onda da particulalivre?


 i ( kxt )
Eop  ( x, t )  i e
  ei ( kxt )   ( x, t )  E ( x, t )
t
A  da partícula livre também é uma autofunção do
operador energia, com autovalor ħ.
Operadorenergia cineticaTop :
 
 

 i   i 
pop pop 
2 2
x 
x 
Top 


2m
2m
2m x 2
Operadorposicao xop  x
Noteque a  da particulalivre nao e' uma autofuncaoda posicao:
x  xei ( kxt )  C
Note que a equação de Schroedinger pode ser escrita em
termos dos operadores:
 2  2  ( x, t )
 ( x, t )

 V ( x , t )  ( x , t )  i
2
2m x
t
Top  Vop   Eop 
Top  Vop  H (operadorHamiltoniano)
H  Eop 
2.4 – Valores Esperados
• Em geral, o resultado de uma medida de uma certa
grandeza física tem uma natureza aleatória: não pode ser
previsto com total certeza.
• Pergunta: qual o valor esperado ou valor mais provável
(do ponto-de-vista estatístico) do resultado de uma medida?
Seja uma certagrandeza fisica Q associada ao operadorQop .
O valoresperado Q da medida no instantet e' dado por :

Q    * ( x, t )Qop  ( x, t ) dx

2.5 – A Equação de Schroedinger independente do
tempo Considerea equacao de Schroedinger quando
o potencialnao depende do tempo: V ( x, t )  V ( x)
 2  2  ( x, t )
 ( x, t )

 V ( x )  ( x , t )  i
2
2m x
t
Novamente,separacaode variaveis:  ( x, t )   ( x) (t )
 2  2 [ ( x) (t )]
[ ( x) (t )]

 V ( x) ( x) (t )  i
2
2m
x
t
1   2 d 2 
1  d 
 V ( x)  i   E

2 
  2m dx 
  dt 
d
d
iE
i
 E 
     (t )  e iEt   e it ( E   )
dt
dt

 2 d 2

 V ( x)  E
2
2m dx
 Equacao de Schroedinger independent e do tempo
Define- se o operadorHamiltoniano :
2 d 2
H  Top  Vop  
 V ( x)
2
2m dx
H  E  Equacao de autovalores
Sua solucao permiteencontraros autovalores
da energia
Exemplos de aplicação da Equação da
Schroedinger em 1D
3.1 – Partícula livre (revisão)
E
Potencial V ( x)  0
 2 d 2
Eq. Schroedinger : 
 E
2
2m dx
Solucoes : ( x)  Aeikx  Beikx
 2k 2
Energias: E 
2m
 2k 2
E
2m
k
Qualquer energia positiva
é permitida (energia varia
de forma contínua)
3.2 – Poço de potencial infinito
V


Potencial:
Região
proibida
Região
proibida
0, 0  x  L
V ( x)  
, x  L ou x  0
0
L
x
Em x  L ou x  0 (regiao proibida):
 ( x)  0
Em 0  x  L, temos V ( x)  0 :
 2 d 2
Eq. Schroedinger : 
 E (comoa particulalivre)
2
2m dx
2 2

k
Solucao :  ( x)  Aeikx  Beikx ; E 
2m
Funcao de onda deve ser continuaem x  0 e x  L
CONDICAO DE CONT ORNO:
 ( 0)   ( L )  0 
Em x  0 :  (0)  A  B  0  A   B
 ( x)  Aeikx  e ikx   Asen kx (a menosde uma constante...)
Em x  L :  ( L)  Asen kL  0  kL  n (n  1,2,3...)
 2 k n2  2  2 n 2
n
kn 
 En 

(energiaquantizada)
2
L
2m
2m L
Funcoesde onda :  n ( x)  Ansen k n x
n : número quântico
V
 (x)
L
0
0
n=2
L
n=3
L
0
L
n=4
Região
proibida
n=1

E3
Região
proibida
0

E2
E1
0
L
x
Comentários de validade
geral:
•Partículas que estão confinadas
a uma região do espaço têm um
espectro discreto de energias, ou
seja, têm energias quantizadas
• Matematicamente, isto decorre
das condições de contorno
impostas nas extremidades (como
numa corda vibrante)
• Quanto maior o número de
zeros (nós) da função de onda,
maior a energia do estado
Exemplo em
nanotecnologia: Poços
quânticos semicondutores
3.3 – Potencial degrau, barreira de potencial e
efeito túnel
Efeito túnel: Atravessando barreiras
P = 100 %
P < 100 %
Barreira
100% - P
Potencial degrau
V
V0
E < V0
E
1
2
0
x
Regiao 1 - eletronlivre:
Regiao 2 - Eq. Schroedinger :
 1 ( x)  Aeikx  Beikx (incidente refletida)
 2 d 2

 V0  E 
2
2m dx
d 2 2mV0  E 

 , V0  E   0
2
2
dx

Solucao : 2 ( x)  Cex  Dex ,
 2k 2
2m E
E
k 
2m

2mV0  E 
onde  

Encontrar B, C e D em termos de A
 1 ( x)  Aeikx  Beikx , x  0
Deve ter derivadascontinuasem x  0 :
 2 ( x)  Cex  Dex , x  0
d 1
dx
Funcao de onda nao pode divergir :
x 0
d 2

dx

x 0
ikA  ikB  D (2)
C 0
Deveser continuaem x  0 :
A  B  D (1)
Combinando(1) e (2),obtemos:
ik  
ik ( A  B )   ( A  B )  B 
A
ik  
ik  
2ik
A
A D D
A
ik  
ik  
Barreira de potencial e Efeito Túnel
 (x)
V
V0
e  x
x
0
incidente
 (x)
refletido
V
transmitido
0
Existe uma probabilidade
de encontrar o elétron na
região classicamente
proibida
a
x
Simulações:
http://www.neti.no/java/sgi_java/WaveSim.html
Se a barreira for
suficientemente pequena
(largura a) o elétron
poderá ser transmitido
(tunelar) com uma certa
probabilidade: EFEITO
TÚNEL
Ptrans   2 (a )  e  2a
2
“Efeito túnel” em ondas clássicas:
Ondas evanescentes
Reflexão interna total
http://wwwhome.math.utwente.nl/~hammerm/Metric/Illust/parcoreM.html
Acoplamento entre
guias de onda
Aplicação em nanotecnologia: STM
(scanning tunneling microscope)
Visualização e manipulação de átomos
Heinrich Rohrer (à esquerda) e Gerd K. Binnig (direita), cientistas do
IBM's Zurich Research Laboratory, na Suíça, receberam
o Prêmio Nobel de Física de 1986 por seu trabalho
no desenvolvimento do microscópio de varredura por tunelamento.
STM
Visualizando átomos
Superfície de Níquel
(IBM Research Labs, California)
Superfície de Silício
(Naval Research Lab,
Wash DC, USA)
Referências:
• “Materiais e Dispositivos Eletrônicos”, Sergio M. Rezende,
Editora Livraria da Física – Seções 2.3, 2.4, 3.1, 3.2, 3.3 e
3.4.
• “Física Quântica”, Eisberg e Resnick, Editora Campus Seções 2.2, 2.3, 2.5, 2.4, Cap. 3, 5.1 a 5.5, 6.1, 6.2, 6.3, 6.5,
6.8 e 6.9
• “Lectures on Physics”, Feynman, Vol. 1, Cap. 37
(interferência com fenda dupla)
Problemas:
Rezende 2.8, 2.9, 2.12, 2.13, 3.2, 3.6, 3.7. 3.9, 3.10
Reproduza os cálculos realizados nesta aula.
Apresentação de Rodrigo Capaz