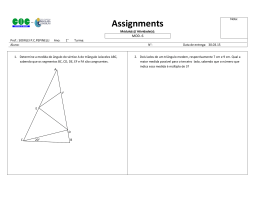
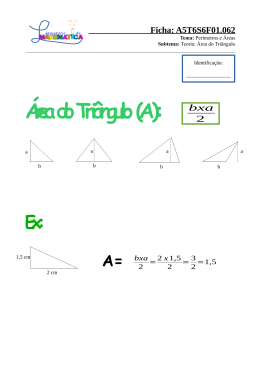
QUESTÃO 03 CEFET 2SEM/2013
Na figura seguinte, representou-­‐se um quarto de circunferência de centro O e raio igual a 2. Se a medida do arco AB é 30o, então, a área do triângulo ACD, em unidades de área, é a)
b)
√!
!
√!
!
c) √2. d) √3. e) √6. Resolução: Ao traçarmos o segmento 𝑂𝐵 (raio), o triângulo 𝐴𝑂𝐵 é isósceles de base AB. Dessa forma os ângulos 𝑂𝐴! 𝐵 e 𝑂𝐵! 𝐴 são iguais. Repare que o triângulo AOD é isósceles. Como 𝐴𝑂 = 𝑂𝐷 = √2 , aplicando Pitágoras em 𝐴𝑂𝐷 , temos que 𝐴𝐷 = 2. No triângulo 𝐴𝐶𝐷, 𝐴𝐷 = 2, 𝐶𝐷 = 1 𝑒 𝐴𝐶 = √3 (Basta aplicar seno ou cosseno) Pronto, como queremos a área do triângulo 𝐴𝐶𝐷, basta fazermos: 1. √3 √3
𝐴∆!"# =
= 2
2
Questão resolvida pelos professores Bruno Ney e Ju Rezende