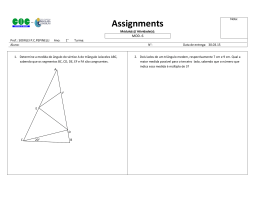
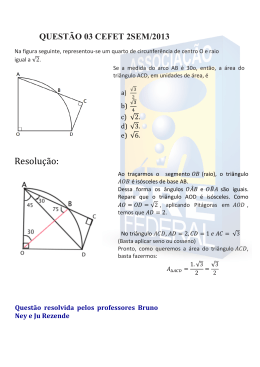
▼ Questão 22 Considere um triângulo isósceles de lados medindo L, L e L centímetros. Seja h a medida da altura relativa ao 2 L . 2 Se L, h e a área desse triângulo formam, nessa ordem, uma progressão geométrica, determine a medida do lado L do triângulo lado de medida L L h L — 2 Resolução Do enunciado, temos a figura, cotada em centímetros: A L L h B H L — 4 C L — 4 L — 2 Aplicando o teorema de Pitágoras ao triângulo retângulo AHB, temos: (AH)2 + (HB)2 = (AB)2 ⎞ L ⎞ 2 = L2 h2 + ⎠4⎠ h2 = 15L2 16 公僓僓僓僓 ∴ h = L 15 4 ⎞ ⎠ Ainda, do enunciado, temos a P.G. L, h, (1) 1 L ⋅ ⋅ h⎞ ⎠ 2 2 Logo, h2 = L ⋅ 1 L ⋅ ⋅h 2 2 De (1) e (2), resulta que 15僓 cm Resposta: 公僓僓 ∴ h= L2 4 (2) 僓僓僓 L2 L公僓1 5 僓. 15 = , ou seja, L = 公僓僓 4 4
Baixar