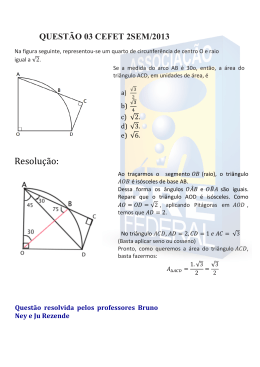
69
Curiosidade
Determinante da matriz e Área de um triângulo
A área do triângulo amarelo é igual à área do rectângulo, reduzida da soma das áreas dos triângulos A, B e C.
Área do rectângulo: ( x2 − x1 )( y2 − y1 )
Área do triângulo A:
1
( x3 − x1 )( y1 − y3 )
2
1
Área do triângulo B: ( x2 − x1 )( y2 − y1 )
2
1
Área do triângulo C: ( x2 − x3 )( y2 − y3 )
2
1
( x2 − x1 )( y2 − y1 ) − [( x3 − x1 )( y1 − y3 ) + ( x2 − x1 )( y2 − y1 ) + ( x2 − x3 )( y2 − y3 )] =
2
Área do triângulo amarelo:
1
= (− x1 y2 − x3 y1 − x2 y3 + x3 y2 + x1 y3 + x2 y1 )
2
Considere-se uma matriz em que nas 1ª e 2ª colunas figuram as abcissas e as ordenadas dos vértices do triângulo ,
⎡ x1
⎢
respectivamente e a 3ª coluna é um vector unitário: x2
⎢
⎢⎣ x3
y1 1⎤
y2 1⎥⎥
y3 1⎥⎦
O determinante desta matriz é: x1 y2 + x3 y1 + x2 y3 − x3 y2 − x1 y3 − x2 y1
A área do triângulo amarelo é metade do valor absoluto do determinante desta matriz
www.moraissilva.com