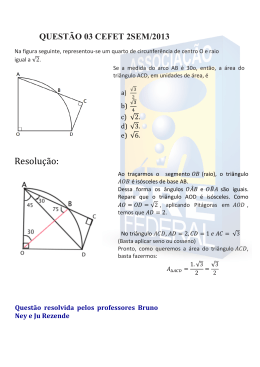
▼
Questão 33

A figura representa um retângulo ABCD, com AB = 5 e AD = 3. O ponto E está no segmento CD de maneira


que CE = 1, e F é o ponto de interseção da diagonal AC com o segmento BE.
Então a área do triângulo BCF vale
D
a) 6
5
E
C
F
b) 5
4
c) 4
3
B
A
d) 7
5
e) 3
2
Resolução
Do enunciado, temos a figura:
1
D
E
H
α
β
C
3 – FG
F
3
FG
β
α
G
A
B
5
Os triângulos AFB e CFE são semelhantes. Logo:
FG AB
FG
5
5
=
=
∴
∴ FG =
FH CE
3 – FG 1
2
Sejam:
S ... área pedida, ou seja, área do triângulo BCF;
S1 ... área do triângulo ABC;
S2 ... área do triângulo ABF.
Temos:
S = S1 – S2
S=
1
1
⋅ AB ⋅ BC – ⋅ AB ⋅ FG
2
2
S=
1
1
5
5
⋅5⋅3 – ⋅5⋅
∴ S=
2
2
2
4
Resposta: b
1