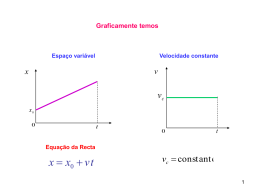
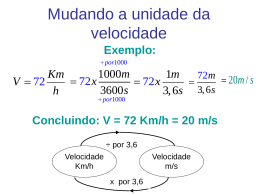
Aula Teórica 5
Introdução aos fluidos em movimento.
Descrição Euleriana e Lagrangeana.
Derivada parcial e material. Aceleração
e aceleração convectiva
Fluidos em Movimento
• No caso de um fluido estar em movimento
existem forças de atrito interno – Tensões de
corte – e pode existir aceleração.
• O estudo dos fluidos em movimento requer o
uso explícito da lei de Newton:



du
F  ma  m
dt
• O estudo dos fluidos em movimento requer
por conseguinte o cálculo da aceleração.
Princípios de conservação
• A mecânica dos fluidos assenta em 3
princípios de conservação: dm
0
• Conservação da massa:
dt
• Conservação da quantidade de movimento:




du d mu  dm
F  ma  m


0
dt
dt
dt
• Conservação da energia:
dQ  dW  dE 
dE dQ dW


dt
dt
dt
Descrição Lagrangeana (1/2)
• Os princípios de conservação aplicam-se a
uma porção de fluido: Sistema Material.
• A aplicação dos princípios de conservação a
um sistema material requer capacidade para
seguirmos uma porção de fluido. Se
conseguirmos, então:






du
F  ma  m
   pndA   mg    dA
dt sup
vol
sup
Descrição Lagrangeana (2/2)
• Quando estudamos o movimento de corpos
sólidos a descrição é sempre lagrangeana.
• À velocidade do corpo e às forças que actuam
sobre ele adicionamos o conhecimento da
posição:

dx 
u
dt
• Na mecânica dos fluidos fazemos o mesmo.
• A dificuldade é identificarmos uma porção de
fluido.....
Descrição euleriana
• É a mais conveniente para o estudo do
movimento dos fluidos, na perspectiva do
utilizador dos resultados.
• Normalmente queremos saber o que se passa
num ponto e não o que se passa com uma
porção de fluido (ao piloto do avião interessa
o que se passa com o avião e não o que fluido
está a passar por ele).
•
Relação entre as descrições





du u u dx u dy u dz




dt t x dt y dt z dt





du u
u
u
u

 ux
 uy
 uz
dt t
x
y
z
ou
dux u x
u x
u x
u x

 ux
 uy
 uz
dt
t
x
y
z
du y u y
u y
u y
u y

 ux
 uy
 uz
dt
t
x
y
z
duz u z
u z
u z
u z

 ux
 uy
 uz
dt
t
x
y
z
A taxa de variação da velocidade de uma partícula de fluido é igual à taxa de
variação da velocidade no ponto onde está a partícula mais a taxa de
deslocamento da partícula vezes a taxa de variação da velocidade no espaço.
Exemplos
• Numa divergência como a
representada ao lado a
velocidade baixa ao longo
do escoamento. Se o
escoamento for
estacionário a velocidade
em cada ponto mantémse constante, mas a
velocidade de uma porção
de fluido baixa.
• A aceleração do fluido é
negativa, a aceleração
local é nula e a aceleração
convectiva é negativa.
Exemplos
• Na atmosfera a aceleração local é
normalmente elevada,
• Num rio a aceleração convectiva é
normalmente elevada, mas a aceleração local
é normalmente baixa.
Forças e acelerações
• Quando a aceleração é elevada, a força
também é!!!
• Porque voa um avião?
Patm
Patm
Considerações finais
• O conhecimento da aceleração permite-nos inferir o
sentido da resultante das forças.
• A curvatura das linhas de corrente dá-nos o sentido
da aceleração e por isso permite-nos ter ideia sobre
a força.
• No caso de haver curvatura, a aceleração tem
componente perpendicular à velocidade e por isso o
gradiente de pressão tem componente perpendicular
à velocidade (a pressão tem que ser maior do lado
de fora da linha de corrente.