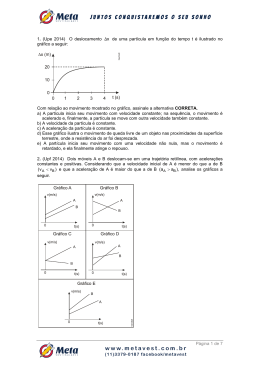
1.VELOCIDADE MÉDIA ESCALAR
02
“ Vm ”
Ex.1 - Uma partícula se deslocando ao longo da reta, figura.
t1  2 s
 40
s1
t2  6s
 20
0
20
s2
40
60
s(m )
Calculo da vm da esfera no intervalo 2s a 6s
vm
60
20  (  40 )
s 2  s1
 15 m/s


 vm 
4
62
t 2  t1
1.VELOCIDADE MÉDIA ESCALAR
Ex. 2
03
“ Vm ”
Um ciclista deslocando-se sobre pista retilínea.
11 12
11
12
10
2
10
2
9
8
3
4
9
8
3
4
7 6 5
7 6 5
s 1  120 k m
s 2  260 k m
s(k m )
A vm do ciclista entre as posições s1 a s2 :
vm
260  120
s 2  s1


 vm 
5,75  3
t 2  t1
140
 50 ,9km / h
2,75
1.VELOCIDADE MÉDIA ESCALAR
Ex. 3
“ Vm ”
(caso 1)
Uma partícula, em movimento retilíneo, apresentou informações
a cerca do seu movimento conforme o diagrama a baixo :
s(k m )
Vm entre 0 e 5 h:
320
vm
160
0
t(h )
2
4
5
S(km)
0
160
160
320
t(h)
0
2
4
5
s3  s0

t3  t0
04

320  0


50
320
 64 km / h
5
1.VELOCIDADE MÉDIA ESCALAR
Ex. 3
“ Vm ”
(caso 2)
Uma partícula, em movimento retilíneo, apresentou informações
a cerca do seu movimento conforme o diagrama a baixo :
s(k m )
Vm entre 2 e 5 h:
320
vm
160
0
t(h )
2
4
5
S(km)
0
160
160
320
t(h)
0
2
4
5
05
s 3  s1


t 3  t1
320  160


52
160
 53,3 km / h
3
1.VELOCIDADE MÉDIA ESCALAR
06
“ Vm ”
Ex. 4
Um móvel percorre uma distância de 200 km em 2,4 h e em seguida
percorre mais 180 km em 1,6 h.
200 k m
Qual a velocidade média
no percurso total ?
180 km
vm
 s total
 s1   s 2


 t total
 t1   t 2
vm
200  180

2,4  1,6

vm

380

 95 k m /h
4
1.VELOCIDADE MÉDIA ESCALAR
07
“ Vm ”
Ex. 5
Um móvel se desloca, sobre trajetória retilínea, e seus espaços
variam no tempo conforme equação “ s = 40 + 2t2 “ no (SI).
Determinar a velocidade média do referido móvel nos intervalos:
A) 0 a 2s
B) 1s a 4s
0
1s
2s
4s
40 m
42 m
48 m
72 m
s 0  4 0  2  0  2  40 m
A
s 2  4 0  2   2  2  48 m
vm 
s
48 - 40

 4m /s
t
2 -0
s 1  4 0  2  1  2  42 m
B
s 3  4 0  2  4  2  7 2 m
vm 
s
72 - 42

 10 m / s
t
4 -1
08
2. CLASSIFICAÇÃO DOS MOVIMENTOS
a. Quanto ao sentido percorrido sobre a trajetória, temos dois tipos de movimentos.
i. Progressivo (s > 0) e (v > 0)
Num movimento progressivo o corpo se desloca a favor da
orientação positiva.

8
4
0
4
o rig e m d o s e s p a ç o s
8
10
14
18
s( m )
09
2. CLASSIFICAÇÃO DOS MOVIMENTOS
a. Quanto ao sentido percorrido sobre a trajetória.....
ii. Retrógrado (regressivo) (s < 0) e (v < 0)
Num movimento retrógrado o corpo se desloca contrário ao da
orientação positiva.

8
4
0
4
o rig e m d o s e s p a ç o s
8
10
14
18
s( m )
10
2. CLASSIFICAÇÃO DOS MOVIMENTOS
b. Quanto a forma da trajetória, temos os movimentos curvos e os retilíneos.
i. Curvilíneo é o movimento cuja direção muda
a cada instante.
Ex. Roda gigante, carrossel, ponteiro de um relógio, movimento de translação da Terra, etc.
Circular
Elíptico
11
2. CLASSIFICAÇÃO DOS MOVIMENTOS
b. Quanto a forma da trajetória, temos os ... e os retilíneos.
ii. Retilíneo é o movimento cuja direção é uma
linha reta.
Ex. Bola de boliche, a queda de um corpo a partir do
repouso, etc.
12
2. CLASSIFICAÇÃO DOS MOVIMENTOS
C. Quanto a variação no módulo da velocidade.
i. Movimento Uniforme (MU) é o movimento
onde a partícula percorre, variações de
espaços “s” iguais, em intervalos de tempo
“t” iguais.
Ex 1.
Uma partícula, deslocando-se sobre trajetória retilínea
teve a seguinte variação de posição no tempo (tabela).
t(s)
s(m)
0
-10
2
0
4
10
6
20
8
30
10
40
12
50
Observa-se que para intervalos de 2s ocorre uma variação de
espaço de + 10m. A velocidade é constante e igual a 5m/s.
14
2. CLASSIFICAÇÃO DOS MOVIMENTOS
C. Quanto a variação no módulo da velocidade.
ii. Movimento Uniformemente Variado (MUV)
é todo o movimento que apresenta variações
de velocidades iguais em iguais intervalos de
tempo. Conseqüência a aceleração escalar é
constante e não nula.
Ex 1.
Um corpo, se desloca em linha reta e apresenta a
seguinte variação de velocidade no tempo (tabela).
t(s)
0
3
6
9
12
15
18
21
v(m/s)
0
6
12
18
24
30
36
42
Observa-se que para intervalos de 3s ocorre uma variação de
velocidade de 6 m/s. A aceleração é constante e igual a 2m/s2.
Definição :
Quando um móvel variou sua velocidade
(V) por um intervalo de tempo (t),
dizemos que este sofreu uma:
A aceleração também é uma grandeza física mista, podendo ser
instantânea (a) ou média (Am)(feita por média ponderada).
-Por motivos da atual grade curricular do novo ensino médio, apenas trabalhamos
com movimentos uniformes variados, logo o modulo da aceleração instantânea e
média, são “sempre” idênticos.
a =
am = V =v - v
t = t - t
Para uma mesma desaceleração, um veiculo leva espaços maiores para parar quando a velocidade é
maior.
Exemplo:Qual a aceleração média de um movimento uniforme variado, de acordo
com a tabela de valores abaixo:
m/s
s
24
0
20
2
16
4
12
6
Am = V : t = (12 – 24):( 6 – 0)= -12 : 6= -2(m/s2)
Obs: Para normas internacionais de
sistemas métricos, exige-se o uso de m/s
para velocidade e m/s2 para aceleração