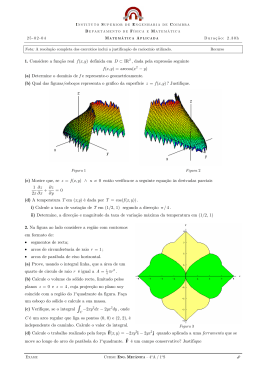
Nota:
Instituto Federal de Educação, Ciência e Tecnologia de São Paulo
Aluno:
PRONTUÁRIO:
Assinatura:
Disciplina:
SISTEMAS DE CONTROLE I
Turma:
Prova: 1
Professor:
Duração:
ALEXANDRE BRINCALEPE CAMPO
Uso de Calculadora:
Sim ( X )
1) Dados os diagramas abaixo:
Não (
)
N6
90 min
Data:
Consulta: Sim ( X )
a) (2,0) Mostre que ambos possuem a mesma função de transferência de malha fechada.
Não (
)
b) (2,0) Supondo que o sistema acima foi denominado J(s)
J (s) =
U (s)
X ( s)
E sabendo que:
H ( s) =
− s + 20
s + 20
F ( s) =
1
( s + 3)( s − 2)
e
K =6
Determine J(s) e seus polos.
c) (2,0) Supondo que J(s) foi inserido no sistema abaixo com:
M (s) =
1
s + 2s + 2
2
(Utilize H(s), F(s) e K do item b)
Determine a faixa de valores de K’ que estabiliza o sistema.
d) (1,0) Sendo R(s) um degrau unitário, determine e4
K ′ = 0,1 para o sistema apresentado no item c).
reg
(Erro estacionário de r(t) em relação a c(t)) supondo que
e) (1,0) Para o mesmo valor de K’ ( K ′ = 0,1 ), determine as constantes de erro estático de Posição (Kp), Velocidade (Kv)
e Aceleração (Ka) para o sistema apresentado no item c). Quais informações estes parâmetros fornecem sobre um
sistema de controle?
2) Em cada um dos sistemas apresentados abaixo (F(s)) foi aplicado um sinal de entrada R(s), sendo obtido o sinal de
saída C(s). Analise cada sistema abaixo quanto à estabilidade, apresentando:
- Os polos da função de transferência F(s);
- Identifique a resposta forçada e a resposta livre em cada caso;
- Analise a resposta do sistema, dado o sinal de entrada, considerando o critério de estabilidade BIBO.
- Afirme em cada caso se o sistema é estável ou não, justificando sua resposta.
a) (1,0) Dados
R( s) =
30
20
e F ( s) = 2
.
( s + 25)
( s + 49)
2
Portanto o sinal de saída pode ser representado no domínio do tempo, após a aplicação da Transformada
Inversa de Laplace, pela seguinte função:
c(t ) = 5 cos(5t ) − 3,57 cos(7t )
b) (1,0) Dados
R( s) =
1
s ( s + 1)
2
e
F ( s) =
1
.
( s + 2 s + 2)
2
Portanto o sinal de saída pode ser representado no domínio do tempo, após a aplicação da Transformada
Inversa de Laplace, pela seguinte função:
c(t ) = 0,5 − 0,2 cos(t ) − 0,4sen(t ) − 0,3e −t cos(t ) + 0,1e −t sen(t )