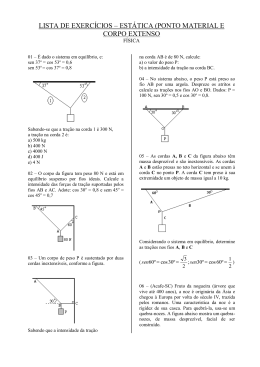
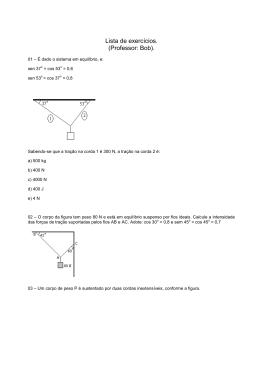
LISTA DE EXERCÍCIOS – ESTÁTICA (PONTO MATERIAL)
01 – É dado o sistema em equilíbrio, e:
sen 37o = cos 53o = 0,6
sen 53o = cos 37o = 0,8
Sabendo-se que a tração na corda 1 é 300 N,
a tração na corda 2 é:
a) 500 kg b) 400 N c) 4000 N d) 400 J e) 4 N
02 – O corpo da figura tem peso 80 N e está em equilíbrio
suspenso por fios ideais. Calcule a intensidade das forças
de tração suportadas pelos fios AB e AC. Adote: cos 30 o =
0,8 e sem 45o = cos 45o = 0,7
05 – As cordas A, B e C da figura abaixo têm massa
desprezível e são inextensíveis. As cordas A e B estão
presas no teto horizontal e se unem à corda C no ponto P.
A corda C tem preso à sua extremidade um objeto de
massa igual a 10 kg.
Considerando o sistema em equilíbrio, determine as
trações nos fios A, B e C
( sen60º  cos 30º 
3
1
; sen30º  cos 60º  )
2
2
06 – Fruto da nogueira (árvore que vive até 400 anos), a
noz é originária da Ásia e chegou à Europa por volta do
século IV, trazida pelos romanos. Uma característica da
noz é a rigidez de sua casca. Para quebrá-la, usa-se um
quebra-nozes. A figura abaixo mostra um quebra-nozes,
de massa desprezível, facial de ser construído.
03 – Um corpo de peso P é sustentado por duas cordas
inextensíveis, conforme a figura.
Sabendo que a intensidade da tração na corda AB é de 80
N, calcule:
a) o valor do peso P:
b) a intensidade da tração na corda BC.
04 – No sistema abaixo, o peso P está preso ao fio AB por
uma argola. Despreze os atritos e calcule as trações nos
fios AO e BO. Dados: P = 100 N, sen 30 o = 0,5 e cos 30o
= 0,8.
Certa noz suporta, sem quebrar, uma força de módulo
igual a 2 000 N. É correto afirmar que, para quebrá-la, a
distância mínima da articulação, d, em cm, onde se deve
aplicar uma força , de módulo igual a 250 N, é:
a) 25. b) 50. c) 20. d) 40.
e) 10.
07 – Para demonstrar as condições de equilíbrio de um
corpo extenso, foi montado o experimento abaixo, em que
uma régua graduada de A a M, permanece em equilíbrio
horizontal, apoiada no pino de uma haste vertical.
Um corpo de massa 60 g é colocado no ponto A e um
corpo de massa 40 g é colocado no ponto I.
Para que a régua permaneça em equilíbrio horizontal, a
massa, em gramas, do corpo que deve ser colocado no
ponto K, é de:
a) 90. b) 70. c) 40. d) 20.
08 – Em um playground de uma escola, duas crianças
brincam em uma gangorra. Ana tem massa de 40 kg e
Beatriz tem massa de 50 kg. A distância do ponto de apoio
para as duas é de 2,0 m. Beatriz permanece na parte de
baixo da gangorra, do lado esquerdo. Ana, por sua vez,
fica na parte alta no lado oposto. Considere g = 10 m/s2.
a) Explique por que Beatriz consegue suspender Ana.
b) Caracterize o torque resultante em relação ao ponto de
apoio.
11 – Suponha que duas crianças brincam em uma
gangorra constituída por uma prancha de madeira de peso
20 kgf. A prancha tem forma regular, constituição
homogênea e encontra-se apoiada em seu centro
geométrico. O peso da criança A é igual a 50 kgf:
Sabendo que o sistema está em equilíbrio na situação
apresentada, determine:
a) O peso da criança B.
b) A intensidade da força exercida pelo apoio sobre a
prancha (reação normal do apoio).
12 – Na figura abaixo está representada uma barra
homogênea de comprimento 3,0 m e peso 60 N em
equilíbrio devido à carga P. Determine o peso da carga P.
09 – Uma barra homogênea de peso B = 200 N está fixa a
uma parede pelo ponto A e por um cabo, conforme mostra
a figura a seguir.
13 – A barra homogênea representada na figura abaixo
tem 3,0 m de comprimento, pesa 600 N e está equilibrada
horizontalmente sobre dois apoios A e B. Determine a
força de reação exercida pêlos apoios sobre a barra.
A carga P tem peso P = 50 N. Considere sen 370 = cos 530
= 0,60. Determine o módulo da tração no cabo.
10 – Em várias situações do dia a dia, necessitamos
aplicar forças que sem o auxilio de alguma ferramenta ou
máquinas, simplesmente não conseguiríamos. Apertar ou
afrouxar um parafuso, por exemplo, requer uma força que
não somos capazes de exercer. Considere um parafuso
muito apertado que necessita da aplicação de um torque
igual a 150 N.m para ser solto, conforme mostra a figura a
seguir.
a) Determine a intensidade da força F aplicada,
desprezado o peso da ferramenta.
b) O que poderia se fazer para reduzir o valor da força
aplicada, encontrada no item a?
14 – 0 sistema da figura abaixo está em equilíbrio. O peso
da carga Q = 20 N e da carga S = 10 N. Desprezando o
peso da barra, determine o peso da carga P.
Gabarito:
1) B
2) TAB = 70,2N
TAC = 61,5N
3) a) P = 40N
b) TBC = 64N
4) TAO = TBO = 100N
5) TA =
6) D
7) B
8) a) Beatriz e Ana têm pesos diferentes e estão a uma
mesma distância do ponto de apoio, logo, Beatriz por ser
mais pesada tem maior torque do que Ana, gerando o
movimento de rotação.
b) M = - 200 N.m. O sentido de rotação é anti-horário.
9) T = 300 N.
10) a) F = 1000 N.
b) Basta usar uma ferramenta com o cabo maior,
aumentando a distância d.
11) a) 100 kgf
b) 170 kgf
12) P = 60 N
13) NA = 450 N e NB = 150 N
14) 55 N