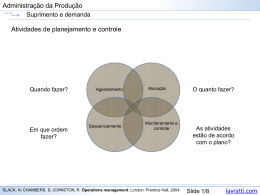
Administração Financeira II
Valor do dinheiro no tempo
Base da Matemática Financeira:
•Fluxo monetário;
•Tempo;
•Equivalência financeira.
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 1/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Fluxo monetário:
•Entradas de saídas de valores monetários;
•Representa os eventos e suas dimensões financeiras;
•Pagamentos e recebimentos ao longo do tempo;
•Para efetuar alguma operação matemática entre eles é necessário utilizar recursos que
compensem suas distâncias.
0
N
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 2/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Tempo:
•O valor monetário sempre está relacionado a um tempo ou período;
•Um valor monetário nominal hoje é diferente desse mesmo valor monetário nominal no
passado ou no futuro.
•Na escala de tempo o 0 (zero ) indica o início e o N indica o final da sequência de tempo
com N períodos iguais.
0
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
N
Slide 3/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Equivalência financeira:
•Fluxos diferentes podem ter o mesmo valor equivalente.
0
N
0
N
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 4/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Fluxo de caixa:
•É uma forma de demonstrar graficamente o que acontece com o dinheiro com o passar
do tempo;
•Facilita a visualização;
•Representa uma aplicação, um investimento, um empréstimo ou um financiamento;
•Mostra as entradas e saídas de dinheiro ao longo do tempo.
0
1
2
3
4
5
6
7
8
9
10
11
12
N
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 5/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Juros:
•Quem tem dinheiro sobrando pode emprestar para quem precisa;
•Por isso, as taxas de juros remuneram o capital investido;
•Portanto, o dinheiro recebido hoje tem mais valor do que a mesma quantia de dinheiro
recebida amanhã;
•Essa é a Teoria da Preferência pela Liquidez;
•Quem tem o direito de receber hoje só aceita deixar para amanhã se o montante
aumentar. As taxas de juros fazem o dinheiro aumentar.
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 6/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Juros:
• JUROS SIMPLES: o juro de cada intervalo de tempo sempre é calculado sobre o
capital inicial emprestado ou aplicado;
• JUROS COMPOSTOS: o juro de cada intervalo de tempo é calculado a partir do
saldo no início de correspondente intervalo. Ou seja: o juro de cada intervalo de
tempo é incorporado ao capital inicial e passa a render juros também.
Taxa de juros
A taxa de juros indica qual remuneração será paga ao dinheiro emprestado, para um
determinado período. Ela vem normalmente expressa da forma percentual, em seguida
da especificação do período de tempo a que se refere:
8 % a.a. - (a.a. significa ao ano)
10 % a.t. - (a.t. significa ao trimestre)
Outra forma de apresentação da taxa de juros é a unitária, que é igual a taxa percentual
dividida por 100, sem o símbolo %:
0,15 a.m. - (a.m. significa ao mês)
0,10 a.q. - (a.q. significa ao quadrimestre)
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 7/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Para compreender um fluxo de caixa:
•Eixo horizontal: linha de tempo;
•Setas para cima: entradas de dinheiro no caixa da empresa;
•Setas para baixo: saídas de dinheiro do caixa da empresa;
•P = capital, principal, quantidade de dinheiro disponível hoje;
•F = valor do dinheiro no futuro;
•A = valor de cada prestação;
•n = número de períodos;
•i = taxa de juros (valor decimal);
•i% = taxa de juros (valos percentual);
•j = taxa de juros acumulada em um período total N (valor decimal);
•j% = taxa de juros acumulada em um período total N (valor percentual);
•J = juros pagos ou recebidos.
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 8/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Juros simples:
Neste caso os juros não são cumulativos. Incidem uma vez em cada período sem
considerar que no período anterior houve pagamento de juros.
J=P.i.n
Exemplo: Temos uma dívida de R$ 1000,00 que deve ser paga com juros de 8% a.m.
pelo regime de juros simples e devemos pagá-la em 2 meses. Os juros que pagarei
serão:
J = 1000 x 0.08 x 2 = 160
F=P.(1+(i.n))
Exemplo: Calcule o montante resultante da aplicação de R$ 70.000,00 à taxa de 10,5%
a.a. durante 145 dias.
F = P . ( 1 + (i.n) )
F = 70000 [1 + (10,5/100).(145/360)] = R$ 72.960,42
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 9/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Juros compostos:
Neste caso os juros são cumulativos. Incidem uma vez em cada período considerando
que no período anterior houve pagamento de juros.
Em um regime de capitalização a juros simples o saldo cresce em progressão aritmética.
F = P . (1 + i)n
Exemplo: Calcule o montante de um capital de R$6.000,00, aplicado a juros compostos,
durante 1 ano, à taxa de 3,5% ao mês.
P = R$6.000,00
t = 1 ano = 12 meses
i = 3,5 % a.m. = 0,035
F = 6000.(1+0,035)12 = 6000. (1,035)12 = R$ 9.066,41
J=F-P
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 10/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
TAXAS EQUIVALENTES
Duas taxas i1 e i2 são equivalentes, se aplicadas ao mesmo capital P durante o mesmo
período de tempo, através de diferentes sistemas de capitalização, produzem o mesmo
montante final.
Seja o capital P aplicado por um ano a uma taxa anual ia.
O montante S ao final do período de 1 ano será F = P(1 + ia )
Consideremos agora, o mesmo capital P aplicado por 12 meses a uma taxa mensal im.
O montante F’ ao final do período de 12 meses será igual a F’ = P(1 + im)12.
Pela definição de taxas equivalentes vista acima, deveremos ter F = F’.
Portanto, P(1 + ia) = P(1 + im)12
Daí concluímos que 1 + ia = (1 + im)12
Com esta fórmula podemos calcular a taxa anual equivalente a uma taxa mensal
conhecida.
Exemplo: Qual a taxa anual equivalente a 8% ao semestre?
Em um ano temos dois semestres, então teremos: 1 + ia = (1 + is)2
1 + ia = 1,082
ia = 0,1664 = 16,64% a.a.
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 11/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
TAXAS NOMINAIS
• A taxa nominal é quando o período de formação e incorporação dos juros ao Capital
não coincide com aquele a que a taxa está referida.
Exemplo: Uma taxa de 15 % a.a., capitalização mensal, terá qual taxa efetiva?
15/12 = 1,25
1,2512 = 1,1608 = 16,08% a.a.
TAXAS EFETIVAS
• A taxa Efetiva é quando o período de formação e incorporação dos juros ao Capital
coincide com aquele a que a taxa está referida.
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 12/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
VALOR FUTURO:
É o quanto valerá o capital no futuro
F = P (1 + i)n
Exemplo: Quanto teremos daqui a 12 meses se aplicarmos R$ 1.500,00 a 2% ao mês?
F = 1500 (1 + 0,02)12 = R$ 1.902,36
VALOR PRESENTE
É o quanto precisamos investir hoje para termos determinado montante no futuro
P = F / (1 + i)n
Exemplo: Quanto devemos aplicar para termos R$ 2.200,00 daqui a 12 meses a 2% ao
mês?
P = 2200 / (1 + 0,02)12 = R$ 1.734,68
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 13/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Tempo de capitalização:
É possível saber quanto tempo será necessário para se obter um determinado montante
n = Log(F/P)/Log(1 + i/100)
Exemplo: Quanto tempo devemos aplicar R$ 3.000,00 para termos R$ 4.886,68 rendendo
5% ao mês?
n = Log(4886,68/3000)/Log(1 + 0,05) = 10 meses
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 14/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Taxa de juros:
É possível saber qual a taxa de juros necessária para se obter um determinado montante
i = (F/P)1/n - 1
Exemplo: Qual a taxa de juros que retorna R$ 10.305,16 para uma aplicação de R$ 5.000
durante 10 meses?
i = (10305,16/5000)0,1 – 1 = 7,5% a.m.
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 15/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Série uniforme de pagamentos:
Um fluxo financeiro pode ser composto de uma série de pagamentos ou recebimentos
idênticos em períodos de tempo iguais.
F = A[(1 + i/100)n – 1]/(i/100)
P = A[1 - (1 + i/100)-n]/(i/100)
A = (P.i/100)/[1 - (1 + i/100)-n]
n = Log[A/(A - P.i/100)]/Log(1 + i/100)
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 16/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Série uniforme de pagamentos:
Valor futuro:
F = A[(1 + i/100)n – 1]/(i/100)
Exemplo: Quanto teremos ao aplicar R$ 200 todo mês durante dois anos a uma taxa de
6% a.m.?
F = 200[(1 + 0,06)24 – 1]/(0,06) = R$ 10.163,12
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 17/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Série uniforme de pagamentos:
Valor presente:
P = A[1 - (1 + i/100)-n]/(i/100)
Exemplo: Quanto teremos que aplicar para receber R$ 300 todo mês durante um ano e
meio a uma taxa de 4,5% a.m.?
P = 300[1 - (1 + 0,045)-18]/(0,045) = R$ 3.648,00
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 18/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Série uniforme de pagamentos:
Valor da prestação:
A = (P.i/100)/[1 - (1 + i/100)-n]
Exemplo: Quanto renderá R$ 10.000 aplicados durante três anos a uma taxa de 5%
a.m.?
A = (10000.0,05)/[1 - (1 + 0,05)-36] = R$ 604,34
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 19/8
lavratti.com
Administração Financeira II
Valor do dinheiro no tempo
Série uniforme de pagamentos:
Tempo:
n = Log[A/(A - P.i/100)]/Log(1 + i/100)
Exemplo: Quanto tempo levará para pagar uma dívida de R$ 5.000 com pagamentos
mensais de R$ 427,68 a uma taxa de 2,5% a.m.?
n = Log[427,68/(427,68 - 5000.0,025)]/Log(1 + 0,025) = 14 meses
Lemes Júnior, A. B. Administração financeira: princípios, fundamentos e práticas brasileiras.
Slide 20/8
lavratti.com