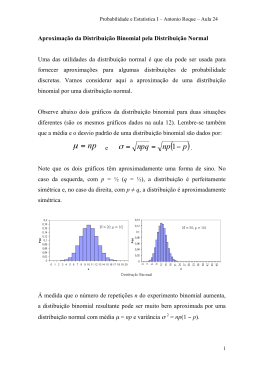
Modelo Binomial para o
cálculo de Opções
Prof. Sérgio Cardoso
Baseado no material do Prof. Luiz Brandão
Modelagem Discreta de MGB
• Os modelos de tempo contínuo exigem uma matemática
relativamente avançada para manipular as equações diferenciais de
valor.
• Podemos, no entanto, modelar estes processos mais facilmente
dividindo o tempo em períodos discretos.
• À medida que adotamos períodos cada vez menores, os valores
obtidos convergem para os valores contínuos.
• Isso é semelhante ao que é feito com o método do FCD, onde
fluxos contínuos são modelados como períodos discretos mensais
ou anuais.
• Em 1979, Cox, Ross e Rubinstein (CRR) desenvolveram um
método discreto que permite desenvolver uma aproximação para o
movimento geométrico browniano.
• Utilizaremos arvores binomiais discretas para modelar projetos
como um Movimento Geométrico Browniano (MGB).
Modelo Binomial de CRR
•
•
•
CRR mostraram que a distribuição de probabilidade lognormal contínua
pode ser modelada através de uma árvore binomial discreta, onde
dS=μSdt+σSdz
Neste modelo, a cada passo o preço (S) é multiplicado por uma variável
aleatória que pode tomar dois valores, u ou d.
Para que essa representação emule uma distribuição lognormal, é
necessário escolher valores apropriados para u, d e a probabilidade p, de
forma que a média (μ) e a variância (σ2) dos retornos de S sejam os
mesmos que os parâmetros do Movimento Geométrico Browniano (MGB)
de S.
Modelo Binomial: Derivação
Modelo Binomial: Derivação
Modelo Binomial: Derivação
Modelo Binomial: Derivação
Modelo Binomial: Derivação
Modelo Binomial de CRR Resumo
Modelo Binomial
Exemplo:
Exemplo
Exemplo
Exemplo
Ex: Solução por Black & Scholes
Ex: Solução por Black & Scholes
Ex: Solução por Black & Scholes
Ex: Solução por Black & Scholes
Ex: Solução por Black & Scholes
Ex: Solução por Black & Scholes
Exemplo
Exemplo
Exemplo