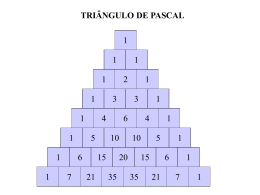
Distribuição
Binomial
Prof. Ivan Balducci
FOSJC / Unesp
O Teorema Binomial
Seja n um nº inteiro não-negativo. Então:
a  b
n
 n  k nk
    a b
k 0  k 
n
O Teorema Binomial
 n  n 0  n  n 1 1  n  n  2 2
( x  a)    x a    x a    x a 
0
1 
 2
n
 n  n j j
   x a
j 0  j 
n
 n  1 n 1  n  0 n

x a  x a
 n  1
 n
Os Coeficientes Binomiais
Para n e k inteiros não-negativos com n  k
 n
n!
  
 k  k!n  k !
Com frequência é lido como
“n escolhe k”.
Exemplos: Cálculo dos Coeficientes
 5
5!
5! 5  4  3! 5  4



 10
 
3!2!
2
 3  3!(5  3)! 3!2!
 20 
20!
20! 20 19 18 17 16 15!


 
15!5!
15  15!(20  15)! 15!5!
20 19 18 17 16 19  3 17 16


 15504
5  4  3  2 1
1


 5  5 
 20   20 
     and     
 3  2
15   5 
Observe que
Lembre que o 1º e o último termo na expansão
n n
têm um coeficiente igual a 1:

1
   
n 0
Observação
a  b
n
 n  k nk
    a b
k 0  k 
n
A soma dos exponentes é sempre n.
Exemplo
x  y 
5
5
 5  k 5 k

  x y
k
k 0  

 5  0 5  5 1 4  5  2 3  5 3 2  5  4 1  5 5 0
   x y    x y    x y    x y    x y    x y
 0
1
 2
 3
 4
 5
 1x 0 y 5  5 x1 y 4  10 x 2 y 3  10 x3 y 2  5 x 4 y1  1x5 y 0
 y  5 xy  10 x y  10 x y  5 x y  x
5
4
2 3
3 2
4
5
Expandindo uma Binomial
Uma binomial é da forma a+b.
Expandindo uma binomial…
( x  a)n
( x  a)0  1
( x  a)1  x  a
( x  a) 2  x 2  2ax  a 2
( x  a)3  x3  3ax 2  3a 2 x  a 3
( x  a) 4  x 4  4ax 3  6a 2 x 2  4a 3 x  a 4
( x  a)5  x5  5ax 4  10a 2 x 3  10a 3 x 2  5a 4 x  a 5
Números Fatoriais

For n  Z ,
n!  n  n  1  n  2  n  3   3  2 1
By convention, 0!  1.
Exemplos
1!  1
2!  2
3!  6
4!  24
5!  120
6!  720
7 !  5040
Exemplos
8!  40320
9!  362880
10!  3628800
11!  39916800
12!  479001600
13!  6227020800
14!  87178291200
Exemplos
15!  1307674368000
16!  20922789888000
17!  355687428096000
18!  6402373705728000
19!  121645100408832000
20!  2432902008176640000
Exemplos
7  6  5  4  3  2 1 7  6  5
7!
7
 7  5  35


  
 3  3!  4! 3  2 1  4  3  2  1 3  2 1
Exemplos
12   12!
 
7!  5!
7
12 11  10  9  8  7  6  5  4  3  2 1

7  6  5  4  3  2 1  5  4  3  2 1
12 11 10  9  8

5  4  3  2 1
 11  9  8
 792
Exemplos
6!
6
  
 6  6!  0!
6  5  4  3  2 1

6  5  4  3  2 1 1
1

1
1
Observações
Sempre um inteiro positivo.
Representa o número de modos de
escolher k items de um grupo de n items.
Pode ser generalizado para valores de n
que não são inteiros.
Fórmula de Bernoulli
Se a probabilidade de sucessos em um
ensaio é p e a probabilidade de fracasso é
q = 1-p, então p e q são constantes de
ensaio a ensaio.
Bernoulli mostrou que a probabilidade de
observar exatamente r sucessos em n
ensaios é expressa pelo r º termo da
expansão para (p+ q)r:
 Pr[r sucessos e n-r fracassos] = (nCr) pr qn-r
Coeficiente Binomial
(
n
) = n!/r!(n-r)!
r
A probabilidade de r sucessos é:
n
( ) pr qn-r ,
r
onde q = 1 - p
Observação
a  b
n
 n  k nk
    a b
k 0  k 
n
Os coeficientes binomiais desta fórmula são os
números da nª linha do triângulo de Pascal.
Cada número é a soma dos números da
esquerda superior e direita superior:
1
1
1
1
1
…
2
3
4
…
1
1
3
6
…
1
4
…
1
…
…
Triângulo de Pascal
 5
 
 0
 
 4
 
0

 3
 
 0
 5
 
1

 2
 
0
 4
 
1

1
 
0
 3
 
1
5
 
 2

0
 
0
 2
 
1
 4
 
 2

1
 
1
 3
 
 2
 5
 
 3

 2
 
 2
 4
 
 3

 3
 
 3
5
 
 4

 4
 
 4

 5
 
 5
 
Linha 0
Linha 1
Linha 2
Linha 3
 5
 
 0
 
 4
 
0

 3
 
 0
 5
 
1

 2
 
0
 4
 
1

1
 
0
 3
 
1
5
 
 2

0
 
0
 2
 
1
 4
 
 2

1
 
1
 3
 
 2
 5
 
 3

k = 0 diagonal
k = 1 diagonal
k = 2 diagonal
 2
 
 2
 4
 
 3

 3
 
 3
5
 
 4

 4
 
 4

 5
 
 5
 
1
1
linha 10
1
1
1
1
1
1
1
1
1
8
9
10
15
70
1
6
21
56
126
252
1
5
35
126
210
4
20
56
1
10
35
84
120
6
15
28
1
3
10
21
36
45
3
5
7
2
4
6
1
7
28
84
210
1
1
8
36
120
1
9
45
1
10
1
Triângulo de Pascal
1
121
1331
14641
1 5 10 10 5 1
1 6 15 20 15 6 1
Teorema Binomial.
Para cada termo,
Obtemos os coeficientes do
Triângulo de Pascal
Triângulo de Pascal
As linhas são os coeficientes da expansão
binomial
Row
#
0
1
1
1
2
1
3
1
4
5
1
1
2
3
4
5
1
1
3
6
10
1
4
10
1
5
1
( x  a)5  x5  5ax4  10a2 x3  10a3 x2  5a4 x  a5
Termos que devem ser familiares
Distribuição Binomial
de probabilidades
Provas de Bernoulli
Triângulo de Pascal