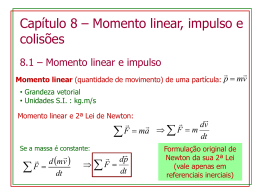
IMPULSO E QUANTIDADE DE MOVIMENTO
1. Impulso de uma força constante
Consideremos uma força constante , que atua
durante um intervalo de tempo sobre uma partícula. O
impulso de nesse intervalo de tempo é uma grandeza
vetorial definida por:
Pela definição, percebemos que os
vetores I e F têm a mesma direção
e o mesmo sentido (Fig.1). A
unidade de impulso não tem nome
especial, sendo expressa em
função das unidades de F e t
Exemplo 1
Uma força F constante, de intensidade F = 20 N, que
atua durante um intervalo de tempo t = 3,0 s sobre o
bloco representado na figura. Determine o impulso de
F nesse intervalo de tempo.
Resolução
Pela definição temos:
O vetor I tem a mesma direção e o
mesmo sentido que F e seu módulo é
dado por:
2. QUANTIDADE DE MOVIMENTO DE UMA PARTÍCULA
Consideremos uma partícula de massa m e velocidade
V (Fig.1). A quantidade de movimento Q da
partícula é definida por:
Pela definição, vemos que a quantidade
de movimento é uma grandeza vetorial.
Além disso, os vetores Q e V têm a
mesma direção e o mesmo sentido.
A quantidade de movimento e também
chamada de momento linear.
Exemplo 1
Uma partícula de massa m = 3,0 kg tem a velocidade V
representada na figura, sendo seu módulo V = 2,0 m/s.
a) Represente a quantidade de
movimento Q da partícula
B) Calcule o módulo de Q
Sendo Q = m.V temos:
3. Impulso de força variável
No caso particular em que a direção da força é constante, é possível
mostrar que o impulso é dado pela área da figura sombreada (Fig.2) no
gráfico de F em função de t.
Exemplo
O impulso de entre os instantes t1
= 1 s e t2 = 4 s, tem módulo dado
pela área da figura sombreada no
gráfico
4. Teorema do Impulso
Consideremos um caso particular, de uma partícula
em movimento retilíneo de modo que a força
resultante F seja constante. Suponhamos que no
instante t1 a partícula tenha velocidade V1 e no
instante t2 a velocidade V2 seja (Fig.3)
I. = .Q
F .t = Q2 – Q1
Esta equação traduz o Teorema de Impulso.
Exemplo
Um bloco de massa m = 2,0 kg tem movimento
retilíneo de modo que a força resultante F tem módulo
dado pelo gráfico a seguir. Sabendo que no instante t1
= 1s, a velocidade do bloco é v1 = 10 m/s, calcule sua
velocidade no instante t2 = 4 s.
Resolução
I = Q
I = Q2 - Q1
60 = (2,0) (v2) - (2,0) (10)
2 v2 = 80
I = m v2 - m v1
60 = (2,0) (v2) - (20)
PRINCÍPIO DA CONSERVAÇÃO DA QUANTIDADE DE
MOVIMENTO
Exemplo
Dois blocos A e B, de massas mA = 6,0 kg e mB = 4,0
kg, movem - se inicialmente sobre uma superfície
horizontal lisa, numa mesma reta, com velocidades
vA = 8,0 m/s e vB = 3,0 m/s, como ilustra a figura.
Como vA > vB, os blocos acabam colidindo e após a
colisão, ficam unidos. Qual a velocidade do conjunto
após a colisão?
Resolução
A quantidade de movimento total antes da colisão,
deve ser igual ao total após a colisão. Depois da
colisão os dois blocos formarão um único corpo de
massa m = 10 kg que move-se com velocidade v.